A Comparative Study of transformer on long sequence time series data

This study evaluates Transformer models in traffic flow prediction. Focusing on long sequence time-series data, it evaluates the balance between computational efficiency and accuracy, suggesting potential combinations of methods for improved forecasting.

Abstract

This research means to discover the power of transformer in dealing with time series data, for instance traffic flow. Transformer with multihead self-attention mechanism is well-suited for the task like traffic prediction as it can weight the importance of various aspects in the traffic data sequence, capturing both long-term dependencies and short-term patterns. Compared to the LSTM, the transformer owns the power of parallelization, which is more efficient when facing a large dataset. And it can capture the dependencies better with long sequences. However, the transformer may have trouble dealing with the long sequence time-series data due to the heavy computation. This research compares differnt methods that make use of the information redundancy and their combination from the perspective of computational efficiency and prediction accuracy.

Introduction

The time series data processing and prediction are usually conducted with RNN and LSTM. In the case of traffic prediction, CNN and GNN are combined for efficiently capturing spatial and temporal information. And LSTM is widely used as its better performance on capturing temporal dependencies. While recent studies have propsed to replace RNNs with Transformer architecture as it is more efficient and able to capture sequantial dependencies. However, the model is inapplicable when facing long sequence time-series data due to quadratic time complexity, high memory usage, and inherent limitation of the encoder-decoder architecture.

Not all time series are predictable, the ones that is feasible to be better forecasted should contain cyclic or periodic patterns. It indicates that there are redundant information in the long sequence data. The coundary of the redundancy can be measured by the optimal masking ratio of using MAE to process the dataset. Natural images are more information-redundant than languages and thus the optimal masking ratio is higher. BERT uses a masking ratio of 15% for language, MAE uses 75% for image and the optimal ratio for video is up to 90%. Traffic data is potentially redundant. It contains temporal and spatial information so that neighbor sensors can provide extra information in addition to temporal consistency. We inducted that the optimal ratio for traffic data should be located between image and video. As it has multidimensional information than image and the speed captured by sensors is not as consistent as the frames in videos. We use the GRIN model to mask the inputdata using Metr_LA dataset to test the redundancy of traffic data. The results show that it is tolerant when the masking ratio is lower than 90%. Then there is the possibility of using distilling operation to compress information, reducing computational requirement and memory usage. Similar to traffic data, most of the time series data are multivariate.

Table 1: Performance comparison with baseline models and GRIN with various masking ratio. (by Tinus A,Jie F, Yiwei L)

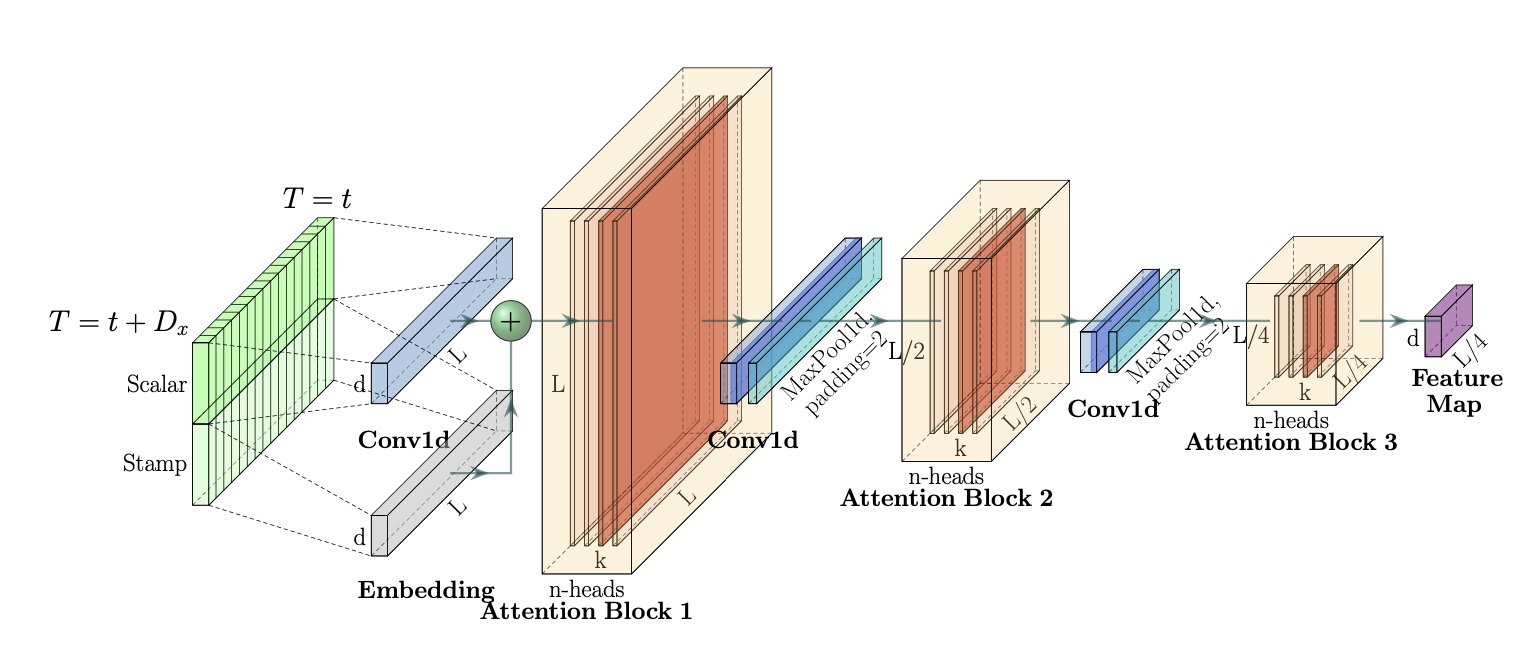
Methodology

The information redundancy leads to the common solutions of using transformer to deal with long sequence time-series forecasting(LSTF) problems, where models focus more on valuable datapoints to extract time-series features. Notable models are focsing on the less explored and challenging long-term time series forecasting(LTSF) problem, include Log- Trans, Informer, Autoformer, Pyraformer, Triformer and the recent FEDformer. There are several main solutions:

Data decomposition. Data decomposition refers to the process of breakking down a complex dataset into simpler, manageable components. Autoformer first applies seasonal-trend decomposition behind each neural block, which is a standard method in time series analysis to make raw data more predictable . Specifically, they use a moving average kernel on the input sequence to extract the trend-cyclical component of the time series. The difference between the original sequence and the trend component is regarded as the seasonal component.

Learning time trend. Positional embeddings are widely used in transformer architecture to capture spatial information. Moreover, additional position embeddings can help the model to understand the periodicity inherented in traffic data, which implies applying the relative or global positioin encoding interms of weeks and days.

Distillation. The Informer model applies ProbSparse self-attention mechanism to let each key to only attend to several dominant queries and then use the distilling operation to deal with the redundance. The operation privileges the superior ones with dominaitng features and make a focused self-attention feature map in the next layer, which trims the input’s time dimension.

Patching. As proposed in ViT, the patch embeddings are small segments of an input image, which transfer the 2D image to 1D sequence. Each patch contains partial information of the image and additional positional embedding helps the transformer to understand the order of a series of patch embeddings. In the case of time series, though it is 1D sequence that can be received by standard transformer, the self-attention may not efficiently capture the long dependencies and cause heavy computation. Hence, dealing with time-series data, patching is used to understand the temporal correlation between data in a time-step interval. Unlike point-wise input tokens, it enhances the locality and captures the comprehensive semantic information in different time steps by aggregating times steps into subseries-level patches.

Experiment

Dataset

We used a multivariate traffichttps://pems.dot.ca.gov/ dataset that records the road occupancy rates from different sensors on San Francisco freeways. We selected first 100 censors as our experiment dataset.

Experimental Settings

We choose two models, Informer and PatchTST(supervised) to test the influence of distillation, positional embeddings, patching and data decomposition. For the implementation of Informer and PatchTST, we used the code provided by the authors.https://github.com/yuqinie98/patchtst. We mean to compare different methods that aim to efficiently explore on long sequence data, considering both efficiency and accuracy. This leads to a discussion about the trade off when using these models to solve real life cases and the possibility of improving or combing different methods.

Figure 1: Informer architecture.

Figure 2: PatchTST architecture.

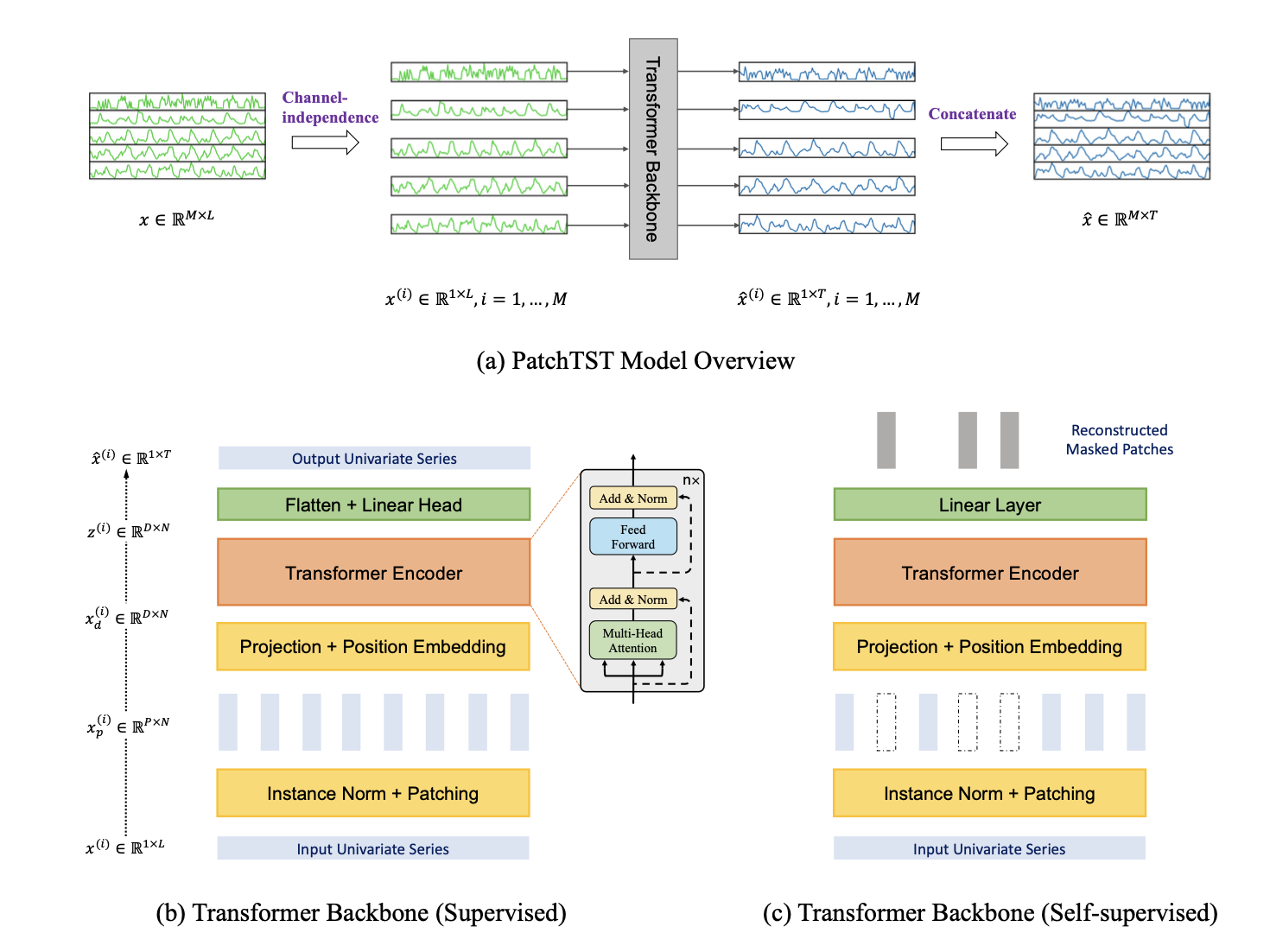
Setting 1. Compare efficieny and accuracy of distillation and patching. All the models are following the same setup, using 10 epochs and batch size 12 with input length \(\in\) {96,192,336,720} and predictioin length \(\in\) {96,192,336,720}. The performance and cost time is listed in the table 2.

Setting 2. Explore the influence of data decomposition. We slightly change the setup to compare different methods. We apply the data decomposition with PatchTST to explore the significance of these techniques.

Result

Table 2: Setting 1. Traffic forecasting result with Informer and supervised PatchTST. Input length in {96,192,336,720} and predictioin length in {96,192,336,720}.

Figure 3: Setting 1. Traffic forecasting result with Informer and supervised PatchTST. Input length in {96,192,336,720} and predictioin length = 720.

Table 3: Setting 2.Traffic forecasting result with supervised PatchTST, with and without data decomposition. Input length = 336 and predictioin length in {96,192,336,720}.

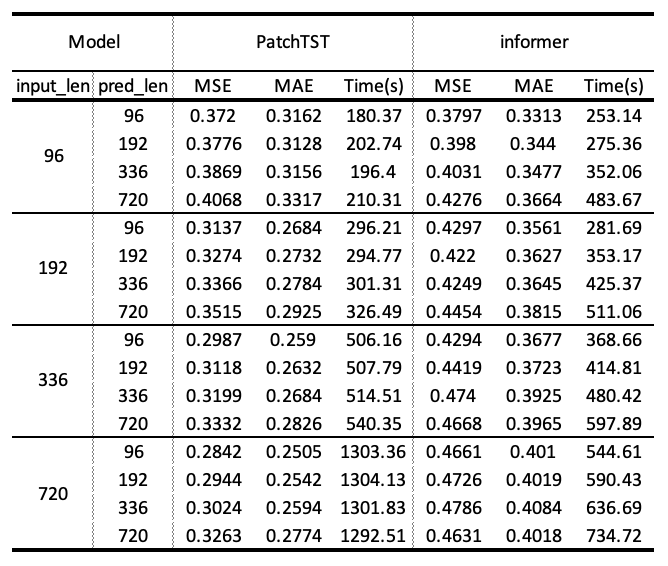
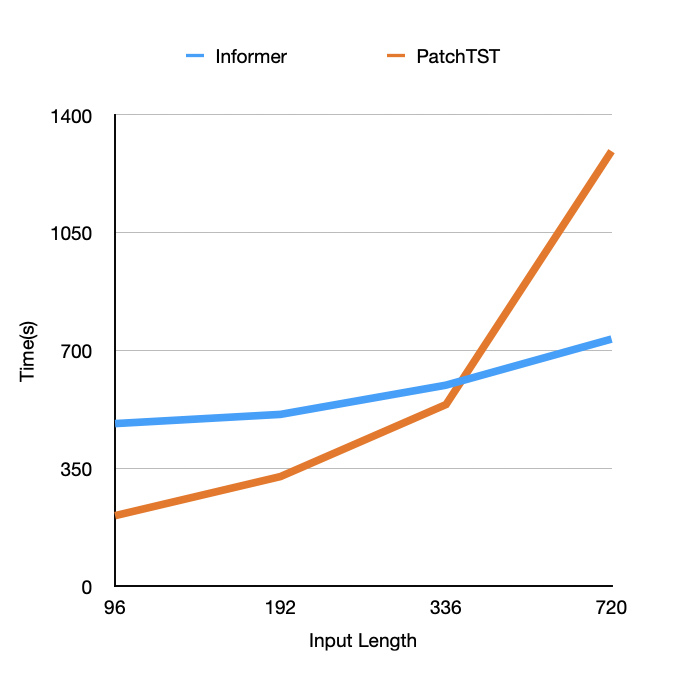
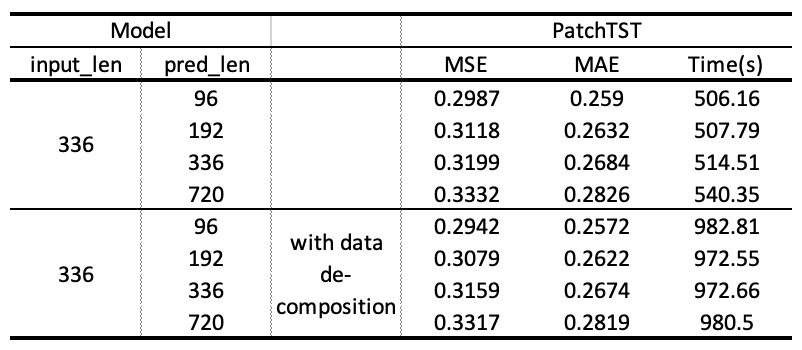
Sufficiency. According to Table 2. The Informer(ProbSparse self-attention, distilling operation,positional embedding) is generally more sufficient than PatchTST(patching, positional embedding). Especially with the increase of input sequence, Informer with idstilling operation can forecast in significantly less time comparing to patching method. Across differnt prediction sequence length, PatchTST does have much difference and Informer tends to cost more time with longer prediction. According to table 3, with data decomposition, PatchTST spends more time while does not achieve significant better performance.

Accuracy. According to Table 2. In all scenarios, the performance of PatchTST is better than Informer considering the prediction accuracy. Along with the increase of input sequence length, PatchTST tends to have better accuracy while Informer stays stable.

Overall, we can induct from the design of two models about their performances. Informer is able to save more time with distilling operation and PatchTST can get better accuracy with the capture of local and global information. Though patch embeddings help the model to get better accuracy with prediction task, it achieves so at the expense of consuming significant amount of time. When the input sequence is 720, PatchTST takes more than twice as long as B.

Conclusion and Discussion

Based on existing models, different measures can be combined to balance the time consumed for forecasting with the accuracy that can be achieved. Due to time constraints, this study did not have the opportunity to combine additional measures for comparison. We hope to continue the research afterward and compare these performances.

In addition to applying transformer architecture alone, a combination of various methods or framework may help us to benefit from the advantages of different models. The transformer-based framwork for multivariate time series representation lerning is proposed by George et al. The Spatial-Temporal Graph Neural Networks(STGNNs) is another widely used model in traffic prediction, which only consider short-term data. The STEP model is propsde to enhance STGNN with a scalable time series pre-training mode. In the pre-training stage. They split very long-term time series into segments and feed them into TSFormer, which is trained via the masked autoencoding strategy. And then in the forecasting stage. They enhance the downstream STGNN based on the segment-level representations of the pre-trained TSFormer.