Emoji3Vec
Our project seeks to expand on the previous attempts at "emoji2vec", or generating semantically meaningful embeddings for emojis.
Introduction
In machine learning, models often create or learn internal representations for the inputs they are given. For instance, an image might become a vector containing the RGB data for every pixel. These internal representations are then processed and transformed until the model finally translates its representation into the desired output form (via softmax over all output possibilities, for example).
The lower dimensional internal representations, known as embeddings, can often carry semantic meaning which can help us understand the data better. Inspired by word2vec, a project for learning embeddings for words, we attempt to learn embeddings for emojis that are semantically interpretable. Learning accurate representations is important for downstream tasks, for example: sentiment analysis and other kinds of classification run better with useful embeddings.
Background and Related Work
Although similar ideas have been explored in the past, we felt that there was still a gap in prior research: specifically, we wanted to create a lightweight model that still learned emoji embeddings directly from data and context.
First, it is important to mention the influential and well known Efficient Estimation of Word Representations in Vector Space, commonly referred to as word2vec
In 2016, a paper called emoji2vec: Learning Emoji Representations from their Description
After considering the above papers, we decided to create a model that would train similarly to word2vec (using naturally sourced data, and from context as opposed to a description) that also was able to produce useful embeddings on smaller amounts of data/memory/training time. Specifically, we felt that the descriptions would err when emojis began to mean different things than they are described as. For instance, the skull emoji is perhaps more often used to indicate embarassment or disagreement than actual death or skulls. This is addressed somewhat in the 2021 Emojional paper, but that one is very limited by the exact words it puts into each emoji’s embedding, and is less adaptable to new meanings. Further, we felt that there was value in creating a more lightweight model that was still able to produce meaningful representations, both to simply be easier to train and run and also to perhaps find optimizations that wouldn’t have been found if we had the option of just training on a larger set of data/training for a longer time.
Methods and Results
We trained two sets of emoji embeddings to map emojis to the same 300-dimensional space as the one FastText uses for its word embeddings. The first was trained on a set of emoji descriptions, with the intention to learn emoji embeddings that reflect the literal appearances of each emoji. We closely follow the methodology as described in the emoji2vec paper to use as a baseline. The second was trained on a set of emoji-containing tweets, with the intention to learn emoji embeddings that reflect how they’re used online.
Training Emoji Embeddings with Descriptions
Data Cleaning
We started with a dataset of emoji descriptions from the Unicode emoji list. After cleaning, we were left with about 6000 descriptive phrases for 1661 emojis within a Python dictionary mapping emojis to various corresponding descriptions. Examples of entries include:
- ‘🐏’: {‘horn’, ‘horns’, ‘male’, ‘ram’, ‘sheep’}
- ‘🆘’: {‘distress signal’, ‘emergency’, ‘sos’, ‘squared sos’}
- ‘👷’: {‘builder’, ‘construction worker’, ‘face with hat’, ‘safety helmet’}
One detail is that we had to generate a bijective mapping between emojis and integers for model training. We encourage those attempting similar projects to save this mapping (in a pickle file, for example) for later use. Leon was very sad when he lost this mapping and couldn’t make sense of his first trained model’s outputted embeddings.

a visualization of how we cleaned our data, from an example of a tweet
Generating Training and Test Data
With a representation learning framework in mind, we randomly generated positive and negative descriptions for each emoji. We defined an emoji’s positive samples as descriptions that truly corresponded to the emoji, and we defined its negative samples as other descriptions in the dataset that weren’t used to describe the emoji. Guided by the emoji2vec paper, we generated positive and negative samples in a 1:1 ratio.
Model Training
After generating positive and negative samples, we used a pretrained FastText model to calculate the average of the embeddings of each word in each description. Put mathematically, if we let the sequence of words in a description be \(w_1, w_2, \dots, w_k\), the set of all strings be \(\mathcal{W}\), and the FastText model be expressed as a mapping \(f: \mathcal{W} \mapsto \mathbb{R}^{300}\), we calculated our description embeddings as
\[\frac{1}{k}\sum_{i=1}^kf(w_i).\]This is a notable deviation from the methodology as described in the emoji2vec paper. Instead of using word2vec embeddings, we chose FastText because it uses sub-word tokenization and thus supports out-of-vocabulary strings as input. We also averaged the description embeddings instead of simply taking a summation to normalize for description length.
#creates a dictionary mapping descriptions to avg. word embeddings
descr_to_embedding = dict()
for descr in all_descriptions:
word_lst = descr.split(' ') #split description into list of words
embed_lst = []
for i in range(len(word_lst)): #repl. words by their embeddings
embed_lst.append(torch.tensor(ft[word_lst[i]]))
avg_embedding = torch.mean(torch.stack(embed_lst, dim=0), dim=0) #take mean over embeddings
descr_to_embedding[descr] = avg_embedding
We again followed the emoji2vec training methodology. For every emoji embedding \(x_i\) and description embedding \(v_i\), the authors model \(\sigma(x_i^T v_j)\) as the probability of the description matching with the emoji, where \(\sigma\) is the sigmoid function. Then our model minimizes the binary cross-entropy loss function
\[\mathcal{L}(x_i,v_j,y_{ij}) = -\log(\sigma(y_{ij}x_i^T v_j + (1-v_{ij})x_i^T v_j))\]where \(y_{ij}\) is 1 when \(v_j\) is a positive sample and 1 otherwise.
The authors don’t describe the exact model architecture used to learn the emoji embeddings, so we likely also deviate in methodology here. Our model is very simple: on some input emoji \(x_i\), we pass it through an nn.Embedding() module, compute \(\sigma(x_i^T v_j)\), and pass it to nn.BCELoss(). This way, the only learnable parameters in the model are in nn.Embedding(), and model training is as efficient as possible.
# the main model class
# follows the Emoji2Vec training
class EmojiDict(nn.Module):
def __init__(self, n_emojis):
# n_emojis: the number of emojis we're learning representations of
super().__init__()
self.embedding = nn.Embedding(
num_embeddings = n_emojis,
embedding_dim = 300 # size of word2vec embedding
)
self.sigmoid = nn.Sigmoid()
def forward(self, x, sample):
# x: a batch of emoji indices, shape (B, )
# sample: a batch of avg'd embeddings, shape (B, 300)
x = self.embedding(x)
# performing a batched dot product
x = torch.unsqueeze(x, dim=1) #(B x 1 x 300)
sample = torch.unsqueeze(sample, dim=2) #(B x 300 x 1)
result = torch.bmm(x, sample) #(B x 1 x 1)
result = torch.flatten(result) #(B, )
result = self.sigmoid(result) #should output probabilities
return result #should be shape (B, )
t-SNE on Learned Embeddings
We trained the model for 60 epochs over a 80-20 train-test split of 250 positive and 250 negative samples for each emoji. We used an Adam optimizer with the default parameters, and model training took roughly an hour. The model achieved 0.19 logloss and 0.98 accuracy on a validation set.
After the model was trained, we took emoji embedding weights from the model’s nn.Embedding() module and projected them down to two dimensions using t-SNE.
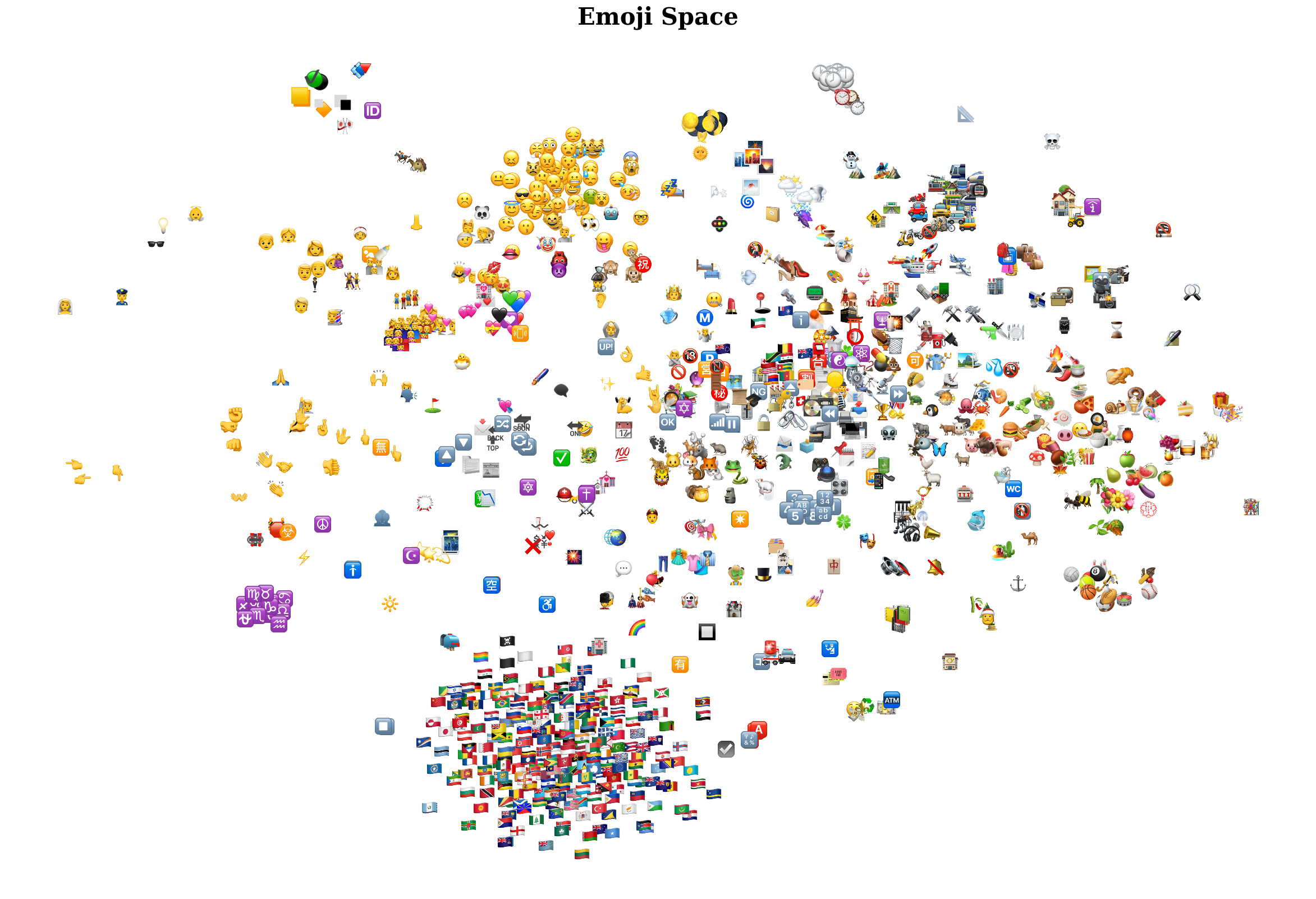
We can see that the model is excellent at grouping emojis that have similar appearances. Nearly all the faces are in the top-left, the zodiac symbols are in the bottom-left, the flags are at the bottom, the foods are on the right, the modes of transportation are in the top-right… the list can keep going. While there are some random emojis scattered about, similar emojis generally are similar in embedding space as well.
Emoji-Emoji Similarities
To confirm this idea quantitatively, we can fix individual emojis and look at its nearest neighbors in embedding space with cosine distance.
| Emoji | 1-NN | 2-NN | 3-NN | 4-NN | 5-NN | 6-NN | 7-NN | 8-NN | 9-NN | 10-NN |
|---|---|---|---|---|---|---|---|---|---|---|
| 😍 | 💖 | 😻 | 😄 | 😀 | 😚 | 💟 | 😘 | 😊 | 😽 | 💑 |
| 😀 | 😄 | 😊 | 😃 | 🙂 | 😑 | 😁 | 😸 | 🤗 | 😆 | 🤧 |
| 💀 | ☠ | 🆎 | 🌫 | 🐁 | ⛓ | ⛸ | 🌮 | 🦅 | ⚖ | 🐙 |
| 🚀 | 🛰 | 👽 | 🚡 | 🛳 | 📡 | 🚢 | 📋 | 🚎 | 🆚 | 🛥 |
We see here that the nearest neighbors also generally make sense. 😍’s nearest neighbors all involve love or positive emotions, and 🚀’s neighbors are generally about space or modes of transport. Interestingly, only 💀’s first neighbor seems remotely similar to it. We believe that this is just because death is a mostly unrepresented theme in emojis.
Word-Emoji Similarities
Since we trained emoji embeddings into the same space as the FastText word embeddings, we can also look at the nearest emoji neighbors to any English word!
| Word | 1-NN | 2-NN | 3-NN | 4-NN | 5-NN | 6-NN | 7-NN | 8-NN | 9-NN | 10-NN |
|---|---|---|---|---|---|---|---|---|---|---|
| happy | 😃 | 😺 | 😌 | 😹 | 🏩 | 😊 | 💛 | 😂 | 😞 | 😁 |
| sad | 😔 | 😭 | 😒 | 🙁 | 😟 | 😞 | 🙍 | 😢 | 😁 | 😯 |
| lit | 🚨 | 🕎 | 🌆 | 🔦 | 📭 | 🎇 | 🕯 | 💫 | 🏥 | 💡 |
| bitcoin | 💛 | 🤑 | 🎮 | 💙 | 🌈 | 🤓 | 📱 | 📅 | 🐰 | 🍆 |
Again, the nearest neighboring emojis generally make sense. Bitcoin’s nearest neighbors are considerably less accurate than the others. Since our nearest neighbors are much more accurate for other English words like “cryptocurrency”, we attribute this inaccuracy to FastText having poor embeddings for “Bitcoin”, which was much less popular word when FastText was trained (in 2015).
One thing to note from these nearest-neighbor tables is that embeddings trained with the emoji2vec method take words very literally. “🚀” is related to space and transportation, and “lit” is related to things that literally light up. As such, these embeddings won’t adjust to semantic changes in emojis as slang develops and people become increasingly clever in their emoji use.
Training Emoji Embeddings with Twitter Data
Data Cleaning
We started with a dataset of emoji-containing tweets. Motivated by the data cleaning done in the emojiSpace paper, we remove duplicate tweets, numbers, hashtags, links, emails, and mentions. Then, we extract the “context” words and emojis around each emoji with a window size of 4 in both directions and tokenize it. We cleaned only a subsample of the tweets due to constraints on memory and compute. Even so, after cleaning, we were left with about 272,000 contexts for 1251 emojis. Examples of contexts for the emoji 🤑 include:
- (‘the’, ‘promotion’, ‘code’, ‘works’, ‘we’, ‘will’, ‘be’, ‘giving’)
- (‘my’, ‘grind’, ‘all’, ‘week’, ‘i’, ‘ain’t’, ‘been’, ‘getting’)
- (‘cash’, ‘in’, ‘on’, ‘sunday’, ‘thank’, ‘you’, ‘so’, ‘much’)
Generating Training and Test Data
With a representation learning framework in mind, we randomly generated positive and negative descriptions for each emoji. We defined an emoji’s positive samples as descriptions that truly corresponded to the emoji, and we defined its negative samples as other descriptions in the dataset that weren’t used to describe the emoji. Guided by the emoji2vec paper, we generated positive and negative samples in a 1:1 ratio.
As in the earlier model, we randomly generated positive and negative contexts for each emoji. We defined an emoji’s positive samples equivalently as before, but this time we used the set of all contexts across all emojis as the set of negative examples. Doing this is obviously not ideal, but it provided a huge performance boost when generating data. Additionally, with such a large dataset, drawing a positive sample as a negative one happens relatively infrequently.
Model Training
The training method we used for this model was nearly identical to that of the first model, and similar to the Continuous Bag-of-Words (CBOW) method for training word2vec. For every context, we calculated the average of the individual word embeddings using FastText. Often, another emoji would be part of the context; such emojis would be passed into the nn.Embedding() module as well to produce an embedding to be passed into the average. The model architecture remained nearly identical, and continued using binary cross-entropy loss as our loss function.
Our model architecture differs somewhat from the original word2vec model, which uses a cross-entropy loss over the entire vocabulary of words as its loss function. While we may lose some expressivity by using binary cross-entropy instead, we believe that making this change made our model more lightweight and easier to train.
# the main model class
# essentially a CBOW on emojis
class EmojiCBOW(nn.Module):
def __init__(self, n_emojis):
# n_emojis: the number of emojis we're learning representations of
super().__init__()
self.embedding = nn.Embedding(
num_embeddings = n_emojis,
embedding_dim = 300 # size of word2vec embedding
)
self.sigmoid = nn.Sigmoid()
def forward(self, x, embeddings, emojis, masks):
# x: a batch of emoji indices, shape (B, )
# embeddings: a batch of summed word embeddings from context, shape (B x 300)
# emojis: a batch of in-context emoji indices, with -1 as a placeholder, shape (B x 8)
# masks: a batch of masks for the relevant emoji indices, shape (B x 8)
x = self.embedding(x)
masks_unsqueezed = torch.unsqueeze(masks, dim=2) # get the dimensions right
emoji_embeddings = self.embedding(emojis * masks) * masks_unsqueezed # apply embeddings to emojis w/ mask applied, (B x 8 x 300)
emoji_embeddings = torch.sum(emoji_embeddings, dim=1) # sum acros embeddings, (B x 300)
tot_embeddings = embeddings + emoji_embeddings # (B x 300)
tot_embeddings = tot_embeddings / 8 # get avg embeddings, could help w/ numerical stability?
# performing a batched dot product
x = torch.unsqueeze(x, dim=1) #(B x 1 x 300)
tot_embeddings = torch.unsqueeze(tot_embeddings, dim=2) #(B x 300 x 1)
tot_embeddings = tot_embeddings.to(torch.float) / 8
result = torch.bmm(x, tot_embeddings) #(B x 1 x 1)
result = torch.flatten(result) #(B, )
result = self.sigmoid(result) #should output target probabilities
return result #should be shape (B, )
t-SNE on Learned Embeddings
We trained the model for 80 epochs over a 80-20 train-test split of 250 positive and 250 negative samples for each emoji. We used an Adam optimizer with the default parameters, and model training took roughly two hours. The model achieved 0.39 logloss and 0.79 accuracy on a validation set.
After the model was trained, we took emoji embedding weights from the model’s nn.Embedding() module and projected them down to two dimensions using t-SNE.

The model does reasonably well at clustering similar emojis together; as before, the flags, faces, and numbers are close together in embedding space. However, the quality of this clustering is noticeably worse than it was in the baseline model. We attribute this to the quality of the dataset and to the increased difficulty in the learning task. The emoji descriptions were clean, precise, and informative; tweets are generally none of those three. Additionally, learning embeddings from contexts has historically required a lot of training data and compute to perform successfully. We, however, only had the compute and memory to sample 500 tweets per emoji, which is only a tiny sample from the massive distribution of possible contexts that may surround any given emoji. Producing emoji embeddings that outperform the baseline model would require much more training data and time than what Colab offers.
While these embeddings lose to the baseline embeddings in overall quality, they have certain properties that the baseline embeddings lack. Namely, since these embeddings were trained on a much more varied and organic dataset, they encode emoji use cases beyond what emojis literally mean. Specifically, they can learn from slang.
Emoji-Emoji Similarities
To illustrate this, we can look at the nearest neighbors of the same four emojis that were presented earlier. We narrow down our search to the top-200 most common emojis in our dataset because those were likely learned the best by our model.
| Emoji | 1-NN | 2-NN | 3-NN | 4-NN | 5-NN | 6-NN | 7-NN | 8-NN | 9-NN | 10-NN |
|---|---|---|---|---|---|---|---|---|---|---|
| 😍 | 🏆 | 💜 | 🎉 | 🇩🇪 | 💘 | 💖 | 👑 | 💞 | 💪 | 🇧🇷 |
| 😀 | 📚 | 😆 | 😏 | 🎉 | 😌 | 😫 | 🔗 | 🙂 | ⚡ | 🇫🇷 |
| 💀 | 😭 | 🍆 | 😓 | 🤤 | 💔 | 😩 | 🐥 | 😮 | 🐻 | 🍑 |
| 🚀 | 💸 | 🔹 | 💯 | 🎯 | 💵 | 2️⃣ | 👋 | 💰 | 😤 | 😎 |
We see here that the nearest neighbors for 😍 and 😀 are noticeably less intuitive than the ones in the baseline model, though some still make sense. Interestingly, however, 💀 has become more associated with strong emotions like 😭 and 😩. This correlates with the online slang “I’m dead,” which expresses a strong (could be both positive or negative) emotional response to something. Additionally, 🚀 has become more associated with money, which correlates with the use of 🚀 to indicate a stock or asset going “to the moon.”
Word-Emoji Similarities
We can also observe this phenomenon in the cosine similarities between words and emojis. We use the same words as above, and again we narrow our nearest neighbors search to the top 200 most popular emojis.
| Word | 1-NN | 2-NN | 3-NN | 4-NN | 5-NN | 6-NN | 7-NN | 8-NN | 9-NN | 10-NN |
|---|---|---|---|---|---|---|---|---|---|---|
| happy | 😃 | 😺 | 😌 | 😹 | 🏩 | 😊 | 💛 | 😂 | 😞 | 😁 |
| sad | 😒 | 😻 | 👏 | 😥 | 😭 | 😓 | 😣 | 😔 | 😂 | 😪 |
| lit | 🔥 | 🚨 | 😍 | ✅ | 😎 | 💯 | 💣 | 🇺🇸 | 🗣 | 💫 |
| bitcoin | 💵 | 🎉 | 😱 | 💸 | 🤑 | 🔹 | 🇮🇳 | 🍃 | 😆 | 🌊 |
As before, the nearest neighboring emojis generally make sense, but are less accurate than the neighbors in the baseline model. At the same time, the nearest neighbors now align more closely with slang (or “new” words like bitcoin). “Lit” now is more related to a feeling of firm agreement, and “bitcoin” is now more related to money. In both cases, the nearest neighbors align more with the words’ common usages than their literal meanings.
Conclusion
Future Work
Given the time and computational constraints we had for this project, we had to pass on many paths for future exploration. We list a few in this section.
-
We would’ve liked to train our second model for much longer on a much larger dataset of tweets. Only about 400 of our emojis had over 50 tweets associated with them. This greatly restricted their positive sample sets, which likely resulted in far-from-optimal emoji embeddings.
-
We also considered training a more expressive neural architecture for our second model. One word2vec CBOW implementation we found used a Linear layer after the Embedding layer. It projected the 300-dimensional embeddings into embeddings with dimensionality equal to the size of the emoji vocabulary to learn embeddings via a multi-class classification problem. We ultimately decided against using such a model because we doubted that we had the time, data, and compute to train a more complex model.
-
Something we realized towards the end of our model training was that the embeddings from the first model could be used to inform training on our second model. It would be interesting to see if transfer learning could result in increased performance for our second model, especially since many emojis were underrepresented in our dataset of tweets.
Discussion
Overall, despite the limitations, our lightweight model achieved reasonable accuracy with less than optimal conditions. One other challenge we faced had to do with Colab’s memory constraints: we were only able to train on a small set of data and were forced to generate positive and negative pairs over and over from the same set. Given a larger and more diverse set of positive/negative pairs, we believe our model could have performed even better.
Furthermore, we felt that our CBOW model definitely could add value for people solving downstream tasks, such as sentiment analysis. The emoji2vec model of summing the emoji’s description’s word embeddings is useful when there are few datapoints for each emoji, but the CBOW approach captures more subtle meanings and is much more accurate to how people actually use emojis in their day to day life—both have their merits.