Graph neural networks v.s. transformers for geometric graphs

With the recent development of graph transformers, in this project we aim to compare their performance on a molecular task of protein-ligand binding affinity prediction against the performance of message passing graph neural networks.

Introduction

Machine learning on graphs is often approached with message passing graph neural network (GNN) models, where nodes in the graph are embedded with aggregated messages passed from neighboring nodes . However, with the significant success of transformers in language modelling and computer vision recently , there are a growing number of transformers developed for graphs as well. In this project we investigate the application of graph neural networks compared to transformers on geometric graphs defined on point clouds. We aim to explore the performance of these two models on predicting the binding affinity for a protein-ligand interaction given the atomic coordinates of the docked protein-ligand structure, which is a highly relevant task in drug discovery. This blog post walks through an introduction into graph neural networks and transformers on molecules, our model architecture, experimental results, and a discussion comparing the two architectures.

Background and relevant work

Graph neural networks on molecules

Graphs are comprised of nodes and edges, and we can model any set of objects with a defined connectivity between them as a graph. For example, social networks are a set of people and the connectivity between them is defined by on who knows who. We can also see that grid data formats, like images, are also graphs where each pixel is a node and edges are defined to the adjacent pixels. Any sequential data, such as text, can be modeled as a graph of connected words. In this section we focus on graphs of molecules where nodes are atoms and edges are defined between atoms. These edges are often defined by the molecular bonds, or for atoms with 3D coordinate information the edges can be defined by a spatial cutoff $d$ based on the Euclidean distance between nodes. Given a graph we can use a graph neural network to learn a meaningful representation of the graph and use these representations for predictive tasks such as node-level prediction, edge-level prediction, or graph-level prediction. Graph neural networks learn through successive layers of message passing between nodes and their neighboring nodes.

An important property of many GNNs applied on 3D molecules is SE(3)-equivariance. This means that any transformation of the input in the SE(3) symmetry group–which includes all rigid body translations and rotations in $\mathbb{R}^3$ –will result in the same transformation applied to the output. This property is important for the modelling of physical systems; for example if the prediction task is the force applied on an atom in a molecule, rotation of the molecule should result in the model predicting the same forces but rotated. In some tasks we do not need equivariance but rather SE(3)-invariance (which is a subset of SE(3)-equivariance) where any transformation of the input in the SE(3) symmetry group results in the same output. This is often the case when the task of the model is to predict a global property of the molecule which should not change if all 3D coordinates of the molecule are translated and rotated. SE(3)-invariance will be required for our model of binding affinity as global rotations and translations of the protein-ligand structure should yield the same predicted binding affinity.

Early SE(3)-equivariant GNNs on point clouds used directional message passing which used the pairwise distance and direction between nodes as features for the GNN, however they were soon shown to be limited in expressivity . Now state-of-the-art (SOTA) models in this area are based on higher order geometric properties such as dihedral angles and representations in the geometric group SO(3). Some examples include GemNet and e3nn . e3nn has also shown that it is much more data-efficient when learning as the model does not need to learn to be equivariant, which non-equivariant models do. For a non-equivariant model to learn to be equivariant it would have to be trained on many SE(3) transformations of the input mapping to the same output, which is very inefficient. e3nn models have led to exceptional performance for tasks related to predicting molecular forces and energies . For the task of binding affinity some GNNs that achieve high performance using GNNs are ProNet and HoloProt .

Graph transformers on molecules

With the proliferation of transformers in the broader field of machine learning, this has also led to the development of graph transformers. In a transformer model each node attends to all other nodes in the graph via attention where the query is a projection of the feature vector of a node, and the key and value is the projection of feature vectors of all other nodes. Hence, graph transformers and transformers applied to sequences (e.g. text) are largely similar in architecture. However, differences arise in the positional encodings in a graph transformer as it is defined in relation to other nodes in the graph . For geometric graphs, positional encodings can be applied as a bias term on the attention value of node $u$ on $v$, where the bias is a learned value that is dependent on the distance between the nodes . There are also other ways of implementing positional encodings in the form of Laplacian eigenvectors, and random walk diagonals which aim to encode the centrality of each node in the graph . Recently, in an effort to unify different methods to generate structural and positional graph encodings, Liu et al. apply a novel pretraining approach with a multiobjective task of learning a variety of positional and structural encodings to derive more general positional and structural encodings. Graph transformers are also achieving SOTA performance for benchmarks on predicting quantum properties of molecules and binding affinity .

Motivation

Given the growing application of both GNNs and transformers we aim to compare their performance on the same task of protein-ligand binding affinity prediction. We also aim to compare models as we can see analogies between graph transformers and GNNs, where “message passing” in the graph transformer involves messages from all nodes rather than the local neighborhood of nodes. We view protein-ligand binding affinity prediction as a suitable task to compare the two architectures as there are aspects of both the GNN and graph transformer architecture that would be advantageous for the task: binding affinity is a global prediction task for which the graph transformer may better capture global dependencies, conversely binding affinity is also driven by local structural orientations between the protein and ligand which the GNN may learn more easily.

Problem definition

Figure 1. A protein-ligand structure, Protein Data Bank (PDB) entry 1a0q. The protein backbone is shown in blue, and the ligand is shown in green. The model would be given this structure and the objective is to predict the binding affinity of the ligand to the protein.

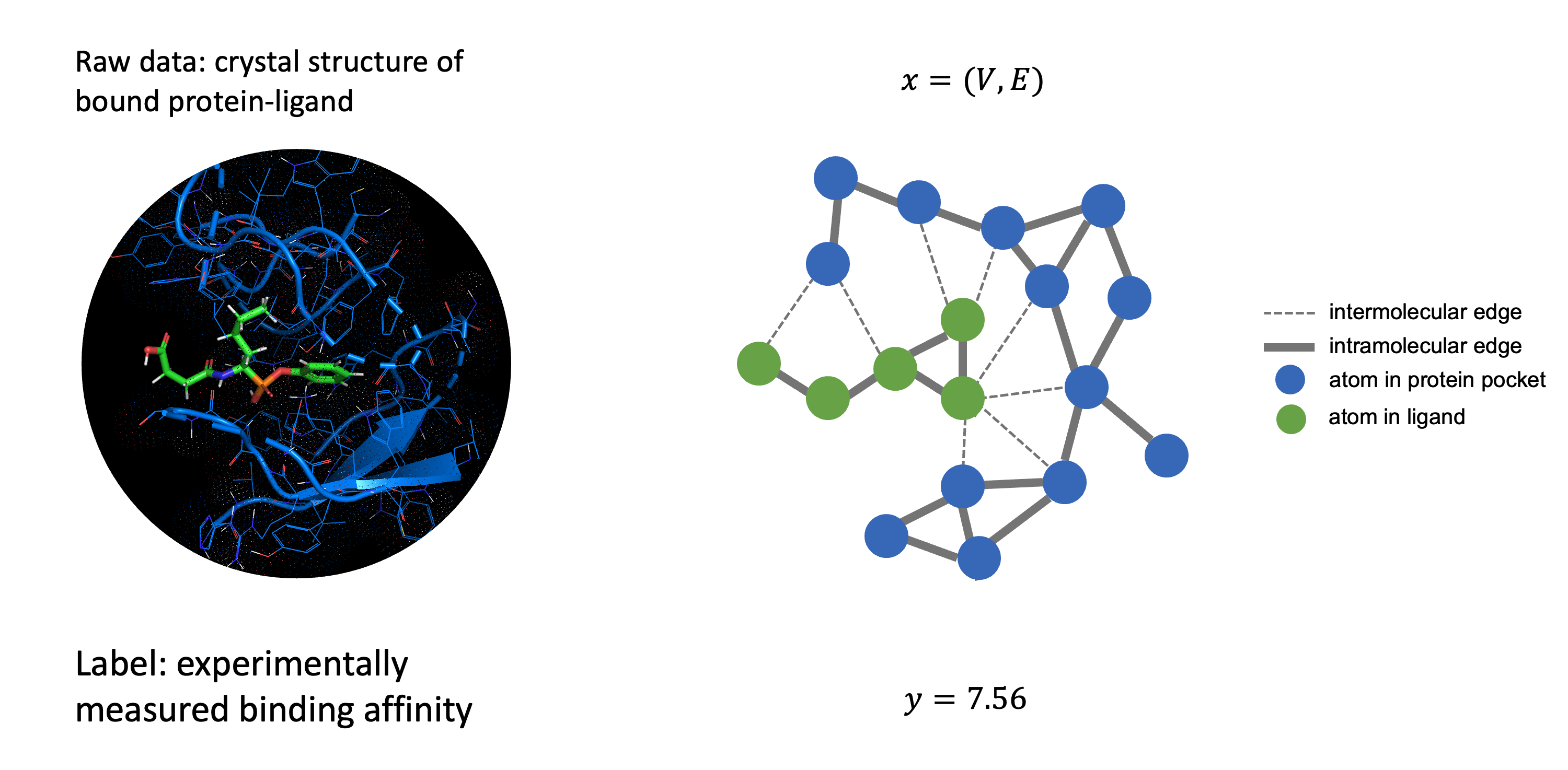
Dataset

We use the PDBbind dataset for the protein-ligand structures and binding affinity. In addition, for benchmarking we use the benchmark from ATOM3D with a 30% and 60% sequence identity split on the protein to better test generalisability of the model. The sequence identity split is based on sequence similarity of proteins in the test and training datasets. The 30% sequence identity split is more challenging are there are more dissimlar proteins in the test set.

Architecture

Graph neural network

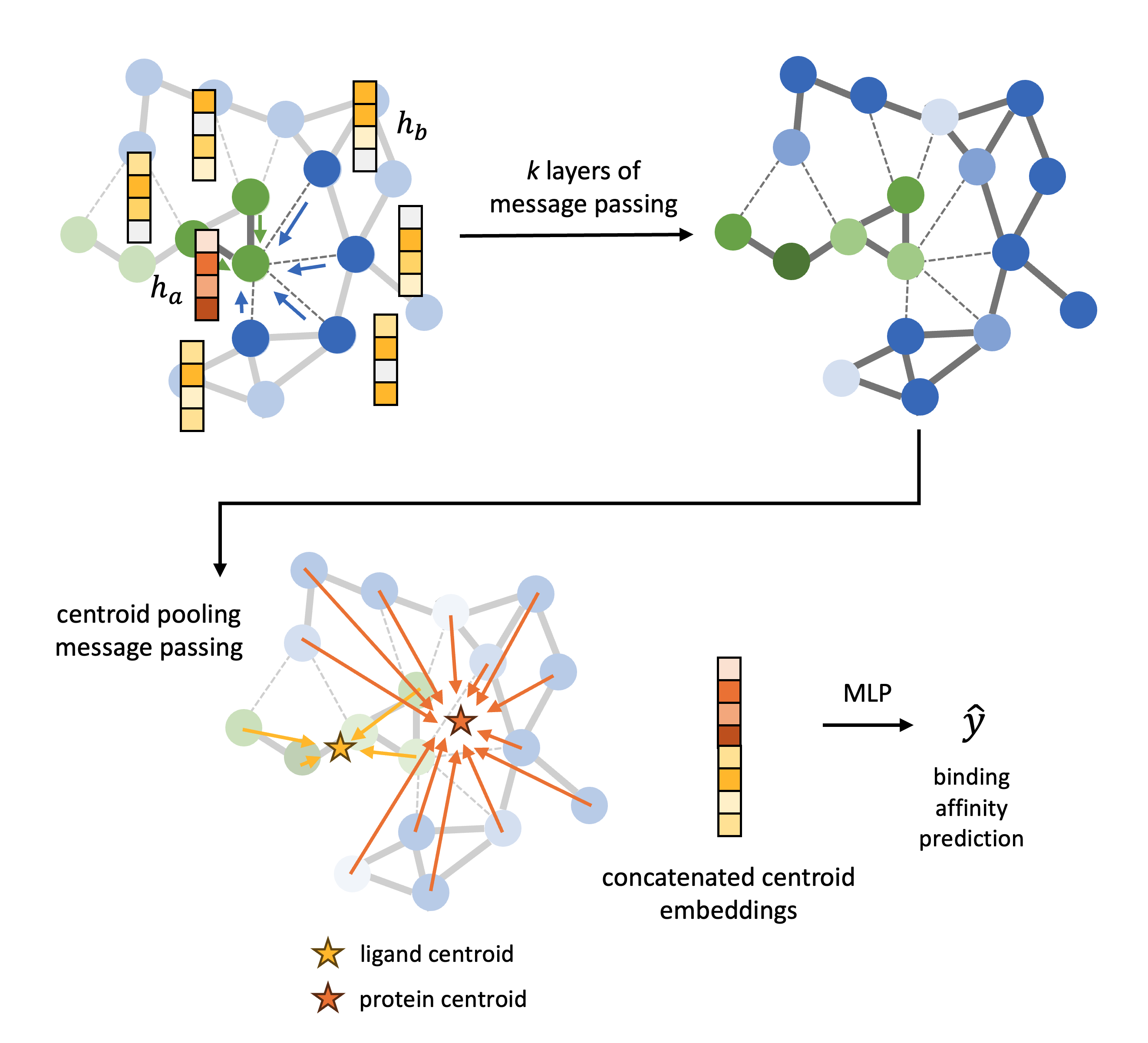
Figure 2. Overview of the GNN architecture for a graph constructed from a protein-ligand structure.

A graph is constructed from the atomic coordinates of the atoms in the protein pocket $X_{\mathrm{protein}}$ and ligand $X_{\mathrm{ligand}}$ where the nodes are the atoms. Intramolecular edges are defined between nodes within $X_{\mathrm{protein}}$ and $X_{\mathrm{ligand}}$ with a distance cutoff of 3 Å, and intermolecular edges for nodes between $X_{\mathrm{protein}}$ and $X_{\mathrm{ligand}}$ with a distance cutoff of 6 Å. The model architecture is defined as follows:

(1) Initial feature vectors of the nodes are based on a learnable embedding of their atomic elements. The edge features are an embedding of the Euclidean distance between the atomic coordinates. The distance is embedded with a Gaussian basis embedding which is projected with a 2 layer MLP.

(2) We define two types of messages in the GNN, given by the two types of edges, intermolecular messages and intramolecular messages. The architecture used for the two types are messages are the same but the weights are not shared, this is to reflect that information transferred between atoms within the same molecule is chemically different to information transferred between atoms of different molecules. 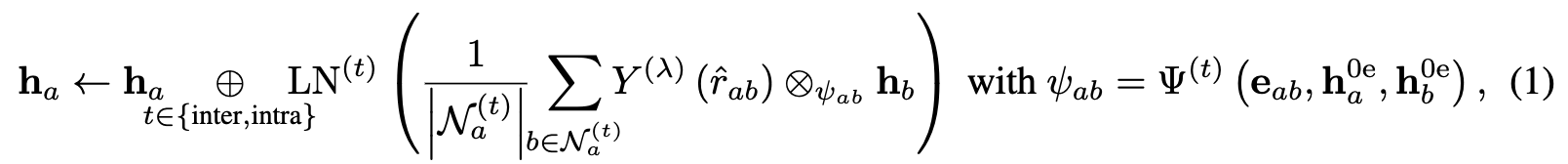The message passing equation uses the tensor product network introduced by e3nn , and our implementation is based on the message passing framework used by DiffDock . We omit the details of the tensor product network for simplicity but provide the overall method below.

where node $b$ are the neighbors of node $a$ in $G$ given by intermolecular or intramolecular edges denoted with $t$. The message is computed with tensor products between the spherical harmonic projection with rotation order $\lambda = 2$ of the unit bond direction vector, \(Y^{(\lambda)}({\hat{r}}_{a b})\), and the irreps of the feature vector of the neighbor $h_b$. This is a weighted tensor product and the weights are given by a 2-layer MLP, $\Psi^{(t)}$ , based on the scalar ($\mathrm{0e}$) features of the nodes $h_a$ and $h_b$ and the edge features $e_{ab}$. Finally, $LN$ is layer norm. Overall, the feature vectors of the nodes are updated by intermolecular and intramolecular messages given by the tensor product of feature vectors of intermolecular and intramolecular neighbors and the vector of the neighbor to the node.

(3) After $k$ layers of message passing we perform pooling for the nodes of $X_{\mathrm{protein}}$ and the nodes of $X_{\mathrm{ligand}}$ by message passing to the “virtual nodes” defined by the centroid of the protein and ligand, using the same message passing framework outlined above.

(4) Finally, we concatenate the embedding of the centroid of the protein and ligand and pass this vector to a 3 layer MLP which outputs a singular scalar, the binding affinity prediction.

Graph transformer

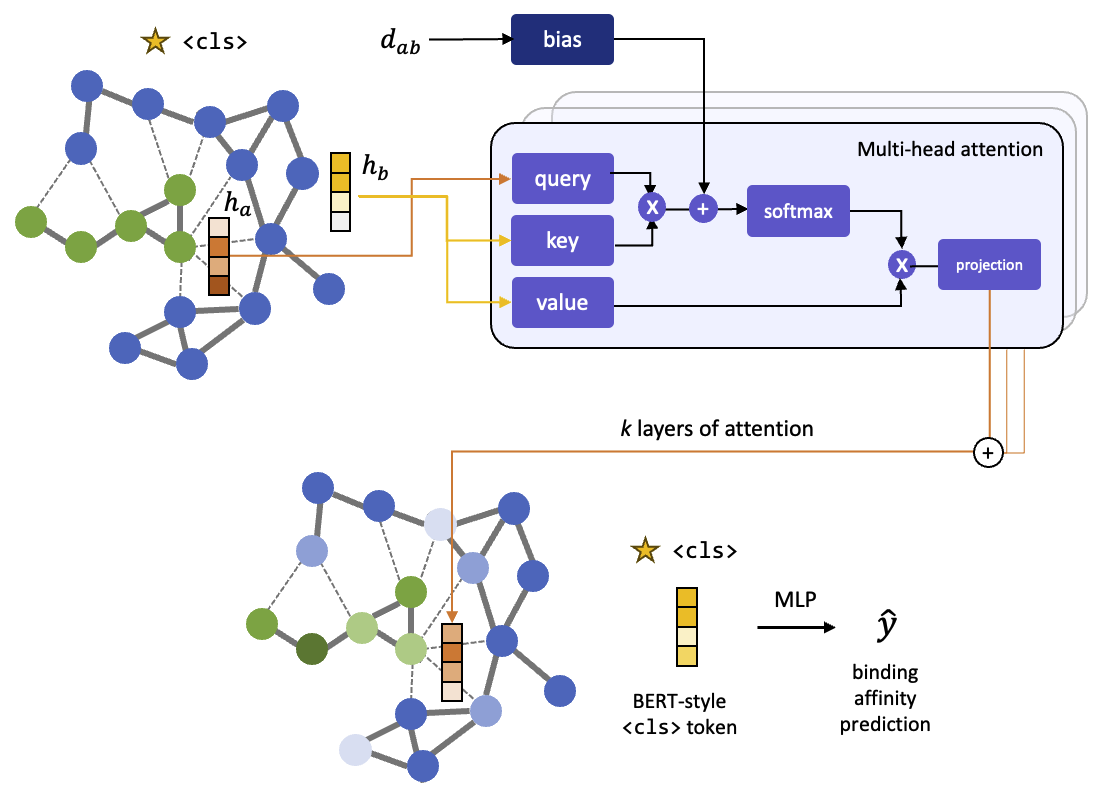
Figure 3. Overview of the graph transformer architecture for a graph constructed from a protein-ligand structure.

The model architecture is as follows:

(1) Initial feature vectors of the nodes are based on a learnable embedding of their atomic elements.

(2) The graph transformer architecture is based on graphormer . Where the input is $H \in \mathbb{R}^{n \times d}$ where $d$ is the hidden dimension and $n$ is the number of nodes. The input is projected by $W_Q \in \mathbb{R}^{d \times d_K}, W_K \in \mathbb{R}^{d \times d_K}, W_V \in \mathbb{R}^{d \times d_V}$. Since graphs have more complex positional information than sequeunces, conventional positional encoding methods used in sequence-based transformers are not applicable to graphs. Positions in a graph are defined relative to all other nodes, thus positional embeddings cannot be added at the node feature vector level but instead are added as a bias to the pairwise node attention matrix. We define $B \in \mathbb{R}^{n \times n}$, where $B_{ij}$ is given by a Gaussian basis embedding of the Euclidean distance $d_{ij}$ between node $i$ and $j$, which is passed to a 3 layer MLP that outputs a singular scalar. Then the self-attention is calculated as $Q = HW_Q, K = HW_K, V = HW_V$ and $A = \frac{QK^T + B}{\sqrt{d_k}}, Attn(H) = Softmax(A) V$. In addition to all atomic nodes, we also add a <cls> token used in the BERT model which functions as a virtual global node . The distance of this node to all other nodes is a learnable parameter. This process is duplicated across multiple heads and we concatenate the embeddings across all heads after $k$ layers as the updated feature vector.

(3) We take the final embedding of the <cls> node and pass it through a 3 layer MLP which outputs a singular scalar, the binding affinity prediction.

Loss function

Both models are trained to minimise the root mean squared error between the predicted binding affinity and true binding affinity.

Experiments

In order for the results to be comparable between the two models, both models have approximately 2.8 million parameters.

GNN model details:

We compare GNNs with different numbers of layers to compare performance across models which learn embeddings from various $k$-hop neighborhoods.

Graph transformer model details: 8 attention heads, 8 layers, hidden dimension = 192, feed forward neural network dimension = 512. Number of parameters: 2,801,155

Both models were trained for 4 hours on 1 GPU with a batch size of 16, Adam optimiser, and a learning rate of $1 \times 10^{-3}$. We show the results for the 30% and 60% sequence-based splits for the protein-ligand binding affinity benchmark in Table 1 and 2 respectively.

Table 1. Protein-ligand binding affinity task with 30% sequence based split. ProNet is included as the SOTA model in this benchmark.

Model Root mean squared error $\downarrow$ Pearson correlation coefficient $\uparrow$ Spearman correlation coefficient $\uparrow$
ProNet 1.463 0.551 0.551
GNN 2 layer 1.625 0.468 0.474
GNN 4 layer 1.529 0.488 0.477
GNN 6 layer 1.514 0.494 0.494
Graph Transformer 1.570 0.476 0.469

Table 2. Protein-ligand binding affinity task with 60% sequence based split. ProNet is included as the SOTA model in this benchmark.

Model Root mean squared error $\downarrow$ Pearson correlation coefficient $\uparrow$ Spearman correlation coefficient $\uparrow$
ProNet 1.343 0.765 0.761
GNN 2 layer 1.483 0.702 0.695
GNN 4 layer 1.471 0.717 0.719
GNN 6 layer 1.438 0.722 0.704
Graph Transformer 1.737 0.529 0.534

Discussion

GNNs perform better than graph transformers

From the benchmarking we can see that the graph transformer model performs worse than the GNNs for the 30% and 60% sequence split for protein-ligand binding affinity. An intuitive explanation for why graph transformers perform worse is it may be difficult for the graph transformer to learn the importance of local interactions for binding affinity prediction as it attends to all nodes in the network. Or in other words, because each update of the node involves seeing all nodes, it can be difficult to decipher which nodes are important and which nodes are not. In order to test if this is true, future experiments would involve a graph transformer with a sparse attention layer where the attention for nodes beyond a distance cutoff is 0. Converse to the lower performance of graph transformers, the results show that deeper GNNs which “see” a larger $k$-hop neighborhood perform better. However, we did not push this to the extreme of implementing a GNN with enough layers such that the $k$-hop neighborhood is the whole graph which would be most similar to a graph transformer as it attends to all nodes. This is because very deep GNNs are subject to issues like oversmoothing where all node features converge to the same value .

The GNN may also perform better than the graph transformer due to the higher order geometric features used by the e3nn GNN message passing framework, compared to the graph transformer which only has relative distances. To further explore this future work will involve implementing the equiformer graph transformer , which is a graph transformer with higher order geometric features.

Depth v.s. width

Deeper GNNs (2 v.s. 4 v.s. 6 layers) with an approximately constant total number of parameters acheived better performance across both protein ligand binding affinity tasks. This was also observed in the image classification field with the development of AlexNet where deeper networks were shown to significantly improve performance . In the context of molecular graphs, deeper GNNs allow the nodes to gain more local chemical context as their node embeddings are exposed to a larger $k$-hop neighborhoods. Thus, these node embeddings are more expressive which facilitates better task performance. There is a limit to the advantages of depth, as very deep GNNs experience oversmoothing as mentioned above .

Model performance v.s. graph size

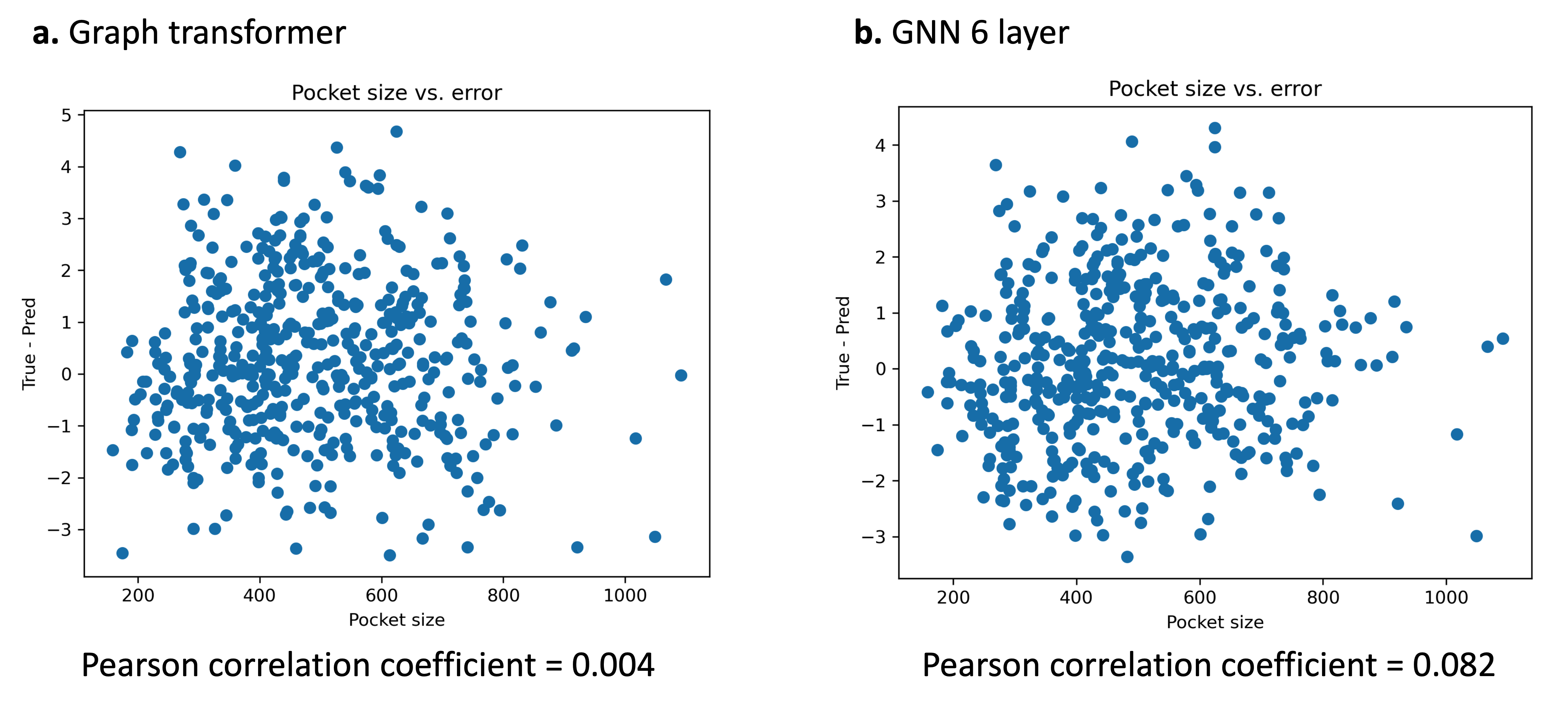
We compared the error of the prediction v.s. the number of atoms in the graph to test the hypothesis if larger graphs are more difficult to make predictions on. However, correlation between error and number of atoms in the graph all yielded very low pearson correlation coefficients ($< 0.1$) for all experiments (Figure 4). Thus, the number of atoms in the graph has minimal effect on the predictive ability of the model. This may suggest why the the graph transformer–which is able to attend to all nodes in the graph–did not perform much better as the GNN performance does not degrade significantly with larger graphs.

Figure 4. Number of nodes in graph v.s. difference between true and predicted binding affinity for graph transformers and GNNs on the 60% protein-ligand binding affinity task. There is no prominent correlation between model performance and error in prediction.

Future work

We implemented a relatively simplistic graph transformer in this project. While we concluded for this vanilla implementation of the graph transformer the GNN outperforms the graph transformer there are many more complex graph transformer architectures that we could explore to build more expressive architectures. In this section we explore some possible ideas.

Using cross-attention for better representation of protein-ligand interactions. In this project, we adapted the graph transformer from graphormer which was developed originally for predicting the energy of one molecule. However, our task involves two interacting molecules, a protein and a ligand. Thus, graph transformer performance could be lifted if the model had a better understanding of the interactions between the protein and the ligand by using cross attention between the protein and the ligand, rather than self attention across the whole protein-ligand complex.

Heirarchical pooling for better representation of amino acids. Graph transformer performance could also be lifted by defining better pooling strategies than using the <cls> token from a set of all atoms to predict binding affinity. In this project the graphs were defined based on the atoms in the graph. However, proteins are comprised of an alphabet of 21 amino acids. Thus, it may be easier for the model to learn more generalisable patterns to the test set if the model architecture reflected how proteins are comprised of animo acids which are comprised of atoms. This has been achieved in models using hierarchical pooling from the atom-level to the amino acid-level and finally to the graph-level .

A hybrid approach: GNNs with Transformers. Finally, we could improve also performance further by taking a hybrid approach. That is, the GNN first learns local interactions followed by the graph transformer which learns global interactions and pools the node embeddings into a global binding affinity value. The motivation for this design is to leverage the advantages of both models. The GNN excels at learning local interactions while the graph transformer excels at learning global relationships from contextualised local interactions. This approach has been explored in other models for predicting drug-target interaction . Visualisation of the attention map of graph transformers would also be interesting to explore the importance of specific chemical motifs on protein-ligand interactions.

Conclusion

In this project we present a direct comparison of graph transformers to GNNs for the task of predicing protein-ligand binding affinity. We show that GNNs perform better than vanilla graph transformers with the same number of model parameters across protein-ligand binding affinity benchmarks. This is likely due to the importance of capturing local interactions, which graph transformers may struggle to do. We also show that deeper GNNs perform better than wider GNNs for the same number of model parameters. Finally, future work in this area will involve a implementing more complex graph transformers, or taking a hybrid approach where we capture local interactions with a GNN and global interactions with a graph transformer.