Zero-Shot Machine-Generated Image Detection using Sinks of Gradient Flows
How can we detect fake images online? A novel approach of characterizing the behavior of a diffusion model's learned score vectors.
Abstract
Detecting AI-generated content has become increasingly critical as deepfakes become more prevalent. We discover and implement algorithms to distinguish machine-generated and real images without the need for labeled training data. We study the problem of identifying photorealistic images using diffusion models. In comparison to the existing literature, we discover detection techniques that do not require training, based on the intuition that machine-generated images should have higher likelihoods than their neighbors. We consider two metrics: the divergence of the score function around a queried image and the reconstruction error from the reverse diffusion process from little added noise. We also compare these methods to ResNets trained to identify fake images from existing literature. Although the previous methods outperform out methods in terms of our accuracy metrics, the gap between our zero-shot methods and these ResNet methods noticeably declines when different image transformations are applied. We hope that our research will spark further innovation into robust and efficient image detection algorithms.
Introduction
As AI-generated images become ever more widespread, garnering virality for how realistic they have become, we are increasingly concerned with the potential for misuse. A deluge of machine-generated fake images could spread misinformation and harmful content on social media. From relatively innocuous pictures of Pope Francis wearing an AI-generated image puffer coat to dangerous disinformation campaigns powered by diffusion models, we live in a new era of media that we cannot trust. The European Union has passed legislation that, among other regulations, requires AI-generated content to be explicitly marked so. The enforcement of such legislation and similar-minded policies, however, remains unclear. Consequently, a growing body of research has sought to develop techniques to distinguish between the real and the synthetic.
The rise of models capable of generating photorealistic content makes the detection problem difficult. While there are still numerous nontrivial challenges with current models from their inability to depict text and render tiny details humans are innately sensitive to such as eyes and hands, the pace of the technology is moving in a way that makes relying on these flaws short-sighted and dangerous. Another potential complication is that advanced photo editing techniques such as Adobe Firefly have capabilities such as generative inpainting that make it such that an image could contain both real and invented content. Even simple data augmentations like crops, rotations, color jitters, and horizontal flipping can make the input look vastly different to a detection model. Furthermore, the majority of popular image generation tools are text-conditional, and we cannot expect to recover the text prompt, not to mention the model that generated the image. This makes transferable, zero-shot techniques of paramount importance.
In this paper, we propose two techniques for detecting images from diffusion models (see Figure 1). Diffusion models
In addition, another metric for the ‘sink’ property of the gradient field at the image of concern is how far the image moves after a small displacement and flow along the gradient field. This has a nice interpretation in diffusion models as the reconstruction error for running the reverse process over just a small timestep on just a slightly perturbed image.
Figure 1: The Divergence and Reconstruction Error Hypothesis: Images on the generated data manifold (red) have negative divergence and small reconstruction error, while images on the real data manifold (green) have zero divergence and large reconstruction error.
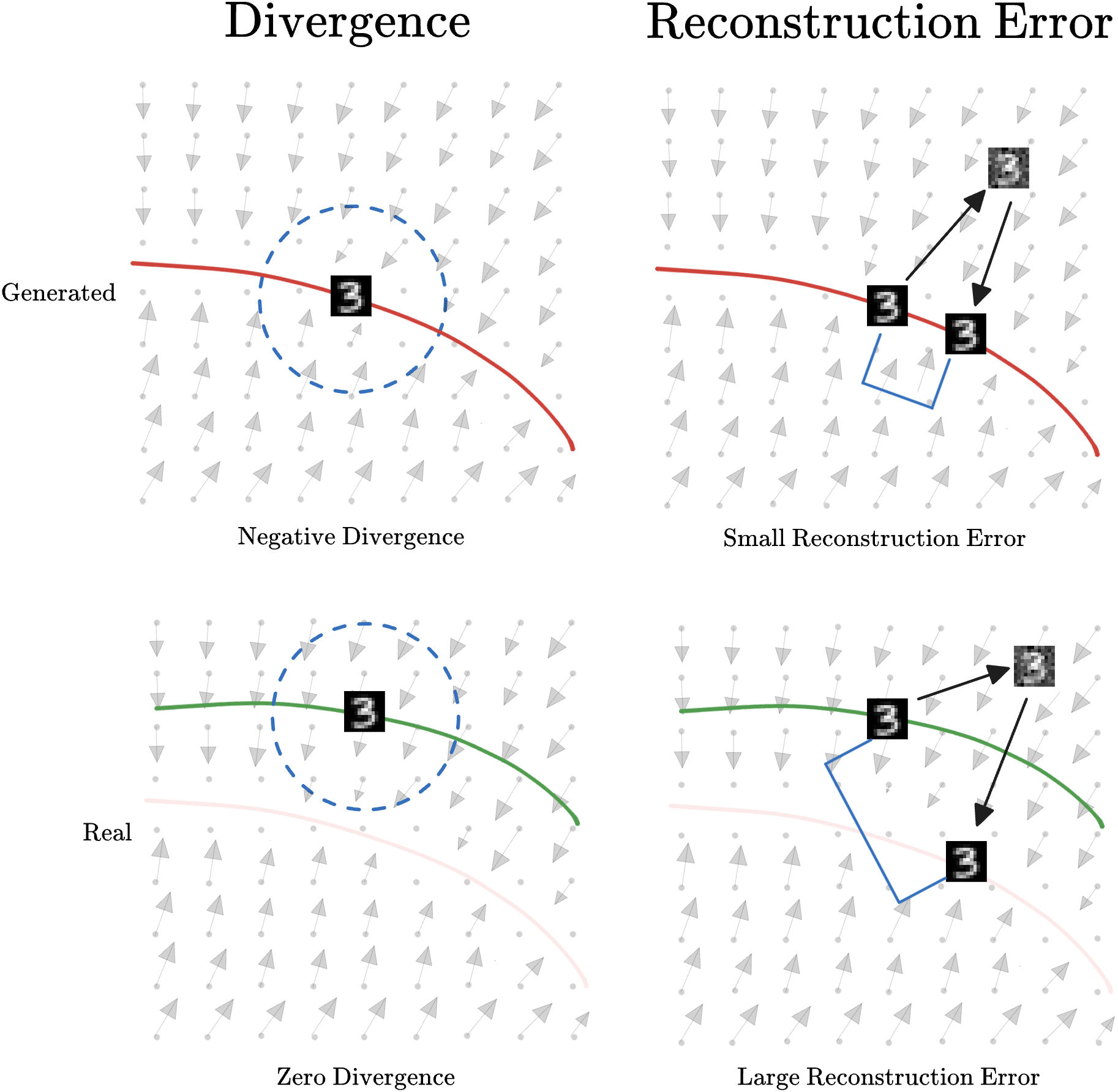
Our overarching research question is thus summarized as, can we use the properties of a diffusion model’s tacit vector field to build an effective zero-shot machine-generated image detector, specifically looking at divergence and reconstruction error?
The main contributions of our paper are:
-
Proposing two methods inspired by sinks of gradient flows: divergence and reconstruction error.
-
Conducting a wide battery of experiments on the performance of these methods in a variety of augmentation settings.
Related Work
Previous literature has considered several different methods for image detection. Sha et al. 2022
We are inspired by ideas from DetectGPT,
where $p_\theta$ is the language model and $q$ is the distribution of perturbations. If the difference in log-likelihood is large, then the attack claims that the original text is more likely to be generated by a language model.
There are several critical differences between language models and diffusion models. With text, one can directly compute the log likelihood of a given piece of text, even with only blackbox access, i.e., no visibility to the model’s parameters. In contrast, for diffusion models, it is intractable to directly compute the probability distribution over images because diffusion models only learn the score. Moreover, the most commonly used diffusion models, e.g. DALL-E 3, apply the diffusion process to a latent embedding space rather than the pixel space. To address the latter concern, we plan on applying the encoder to the image to obtain an approximation of the embedding that was passed into the decoder. And to address the former, instead of approximating the probability curvature around a given point like DetectGPT, we formulate a statistic characterizing whether the gradient field/score is a sink, i.e., the gradients around a machine-generated image point to the machine-generated image. This captures the idea of a local maximum in probability space, similar to the DetectGPT framework.
It would be remiss to not mention Zhang et al. 2023,
Methods
Dataset. To conduct our research, we needed datasets of known real and fake images. We used MSCOCO
Baseline. We used the model and code from Corvi et al. 2023
Detection Algorithms. For out attacks, we compute the divergence of the diffusion model’s score field around the image (negative divergence indicates a sink). We can estimate this via a finite-differencing approach: given a diffusion model $s_\theta(x)$ which predicts the score $\nabla_x\log p_\theta(x)$, we have that
\[\mathrm{div}(s_\theta,x)= \sum_{i=1}^d \frac{s_\theta(x+he_i)_i-s_\theta(x-he_i)_i}{2h}\]for small $h$ and orthogonal basis ${e_i}_{i=1}^d$. However, images are high-dimensional, and even their latent space has $\approx10,000$ dimensions, which means that fully computing this sum could be computationally expensive. In this paper, we sample a fraction of the dimensions for each queried image.
Another way to capture the intuition that machine-generated images are have higher likelihoods than their neighbors is by noising the latent to some timestep $t$, and then comparing the distance of the denoised image to the diffusion model to the original image. That is, given a diffusion model $f_\theta$ which takes a noised image and outputs an unnoised image (abstracting away noise schedulers, etc. for clarity),
\[\mathrm{ReconstructionError}(f_{\theta},x)\triangleq \mathbb{E}_{\tilde{x}\sim \mathcal{N}(x,\epsilon)}||x-f_{\theta}(\tilde{x})||_2^2\]for small $\epsilon$. The intuition is that if an image and thus more likely, then the denoising process is more likely to send noisy images to that particular image.
Comparison. For each model, we use the AUC-ROC curve and the true positive rate (TPR) at low false positive rate (FPR) as metrics. The latter notion of accuracy is borrowed from the membership inference attack setting in Carlini et al. 2021.
Experiments
We run all experiments over a common set of 500 images from the test set of MSCOCO and the corresponding 500 images generated by Stable Diffusion V1.4 with the same prompt using HuggingFace’s default arguments.
For our Divergence method, we randomly sample $d=10$ dimensions to compute the divergence over and set $h=0.1$. For our Reconstruction method, we compute an average distance over 10 reconstructed images per original image and use add/remove noise equivalent to 1 time-step.
For each method, we evaluate the performance on no augmentation, random $256\times 256$ crop (corresponding to about a quarter of the image for generated images), grayscale, random horizontal flip with probably $0.5$, random rotation between $[-30^\circ,30^\circ]$, and random color jitter of: brightness from $[0.75,1.25]$, contrast from $[0.75,1.25]$, saturation from $[0.75,1.25]$, and hue from $[-0.1,0.1]$.
Table 1: Divergence, Reconstruction, and ResNet Detection AUC and True Positive Rate at 0.1 False Positive Rate.
| AUC / TPR$_{0.1}$ | Method | ||
|---|---|---|---|
| Augmentation | Divergence | Reconstruction | ResNet |
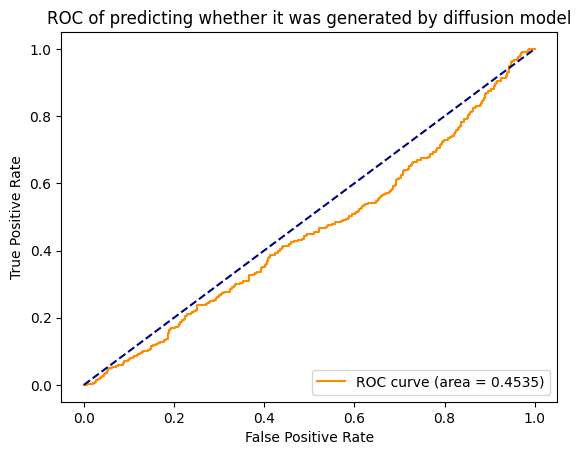
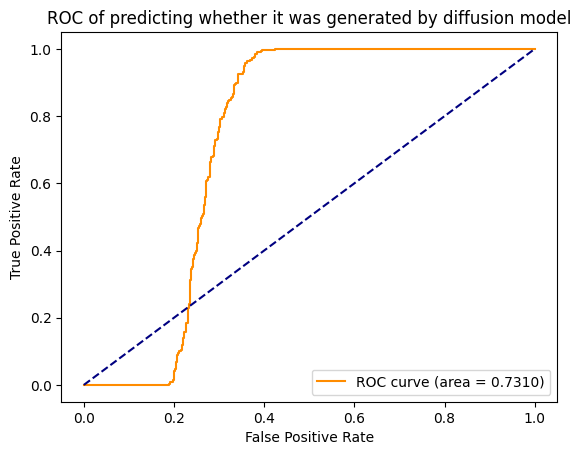
| No Aug. | 0.4535 / 0.078 | 0.7310 / 0.000 | 1.000 / 1.000 |
| Crop | 0.4862 / 0.092 | 0.4879 / 0.064 | 1.000 / 1.000 |
| Gray. | 0.4394 / 0.056 | 0.7193 / 0.000 | 1.000 / 1.000 |
| H. Flip | 0.4555 / 0.084 | 0.7305 / 0.000 | 1.000 / 1.000 |
| Rotate | 0.4698 / 0.062 | 0.6937 / 0.000 | 0.9952 / 0.984 |
| Color Jitter | 0.4647 / 0.082 | 0.7219 / 0.000 | 1.000 / 1.000 |
Figure 2: AUC-ROC Curves in No Augmentation Setting.
(a) Divergence
(b) Reconstruction
(c) ResNet
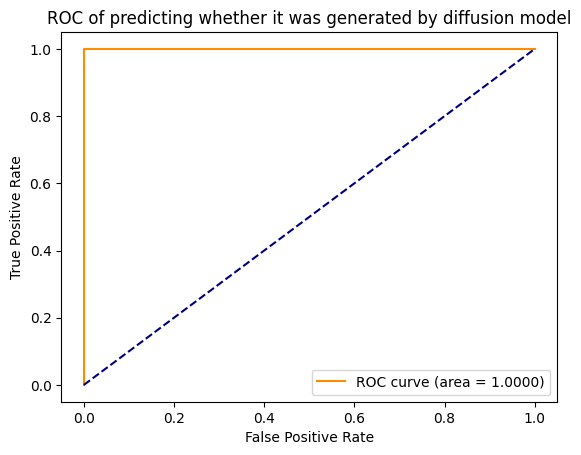
Figure 3: Histograms of Computed Statistics in No Augmentation Setting.
(a) Divergence
(b) Reconstruction
(c) ResNet
Trained Baseline. The trained baseline does extraordinarily well at the MSCOCO vs. Stable Diffusion detection task. It achieves $1.0$ AUC (perfect accuracy) across all augmentation settings except for rotation for which it gets an almost perfect AUC of $0.9952$. This high performance matches Corvi et al. 2023’s findings,
Divergence. Divergence does extremely poorly, with AUCs just slightly below 0.5, indicating that in fact generated images have greater divergence than real images—the opposite of our intuition, but this may also be noise as these values are essentially equivalent to random guessing. We suspect that this is largely due to our low choice of $d$, meaning that we cannot get a representative enough sample of the dimensions to get an accurate estimate of the true divergence. We may have also chosen $h$ too large, as we have no idea of the scale of any manifold structure that may be induced by the gradient field.
Reconstruction Error. Reconstruction error, on the other hand, boasts impressive AUCs of around $0.7$. The shape of the curve is particularly strange, and with the additional observation that the AUC when the random cropping is applied goes back to $0.5$ AUC, indicated to us that the image size may be the differentiating factor here. MSCOCO images are often non-square and smaller than the $512\times 512$ constant size of the generated images. As the Frobenius norm does not scale with image size, we hypothesize that using the spectral norm and dividing by the square root of the dimension would instead give us a more faithful comparison, akin to the random crop results. However, data visualization of the examples does not show a clear correlation between image size and reconstruction error, so it appears that this detection algorithm has decent AUC but poor TPR at low FPR, and is vulnerable to specifically cropping augmentations.
Detection Visualizations. We developed a dashboard visualizaiton that enables us to look more closely at images and their associated detection statistics. Some examples we can pick out that seem to make sense include Figure 4, where the real image is captioned as a CGI fake image, and predictably gets a low statistic as deemed by Reconstruction Error (the generated image, ironically, gets a higher statistic denoting more real).
Figure 4: An Example Image of a CGI “Real” Image Getting Detected as Fake.
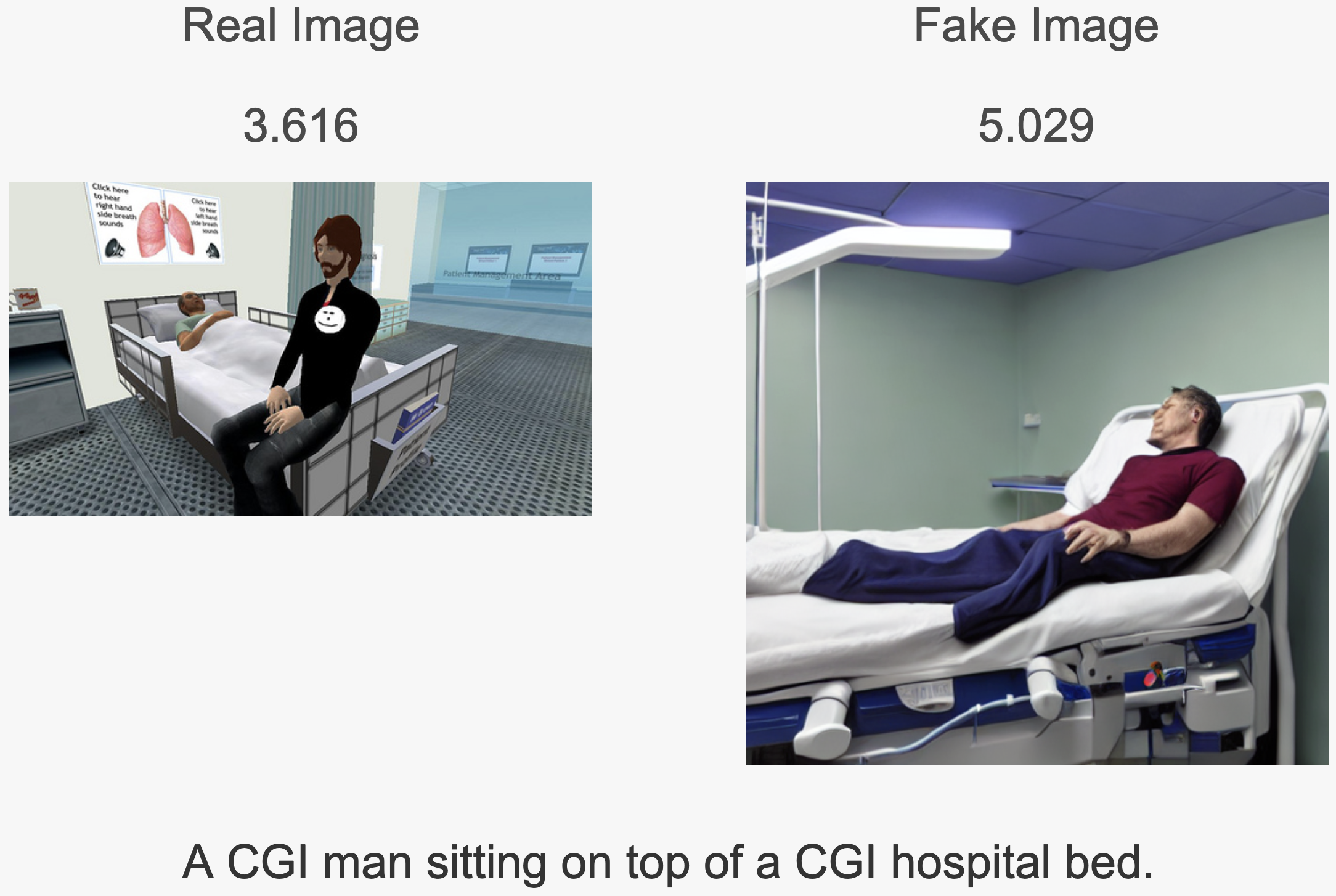
However, from a visual inspection of images, we cannot identify a clear relationship between image content or quality of generated images that holds generally. We make our dashboard public and interactive; a demo can be seen below:
Discussion
Throughout our experiments, the divergence-based detector performs much worse than the other detectors. Because the latent space has a very high dimension, the divergence detector may require sampling from many more dimensions than is practical for an image detector in order to obtain good estimates of the divergence. Further research should try to scale this method to see if it obtains better results. Mitchell 2023 et al.
Although at face-value our detectors perform worse than the pre-trained model in our experiments, our project still introduces some interesting ideas for machine-generated image detection that are of interest to the broader community and worth further exploring. First, the techniques we explored parallel zero-shot machine-generated image detection methods for text.