Comparing data augmentation using VAEs and denoising-VAEs for limited noisy datasets

Background

One of the significant challenges in this evolving landscape of machine learning is the prevalance of limited and noisy datasets. Traditional models and downstream tasks such as classification often struggle with such datasets, leading to suboptimal performance and a lack of generalizability.

Could this be tackled using auto-encoders, specifically, Denoising Autoencoders (DAE) and Variational Autoencoders (VAE)? Denoising autoencoders (DAE) are trained to reconstruct their clean inputs with noise injected at the input level, while variational autoencoders (VAE) are trained with noise injected in their stochastic hidden layer, with a regularizer (KL divergence) that encourages this noise injection. But what if we could combine these strengths?

Motivation

Denoising autoencoders (DAE), are trained to reconstruct their clean inputs with noise injected at the input level, while variational autoencoders (VAE) are trained with noise injected in their stochastic hidden layer, with a regularizer (KL divergence) that encourages this noise injection. Denoising Variational Autoencoders (DVAEs) are an extension of the traditional variational autoencoder (VAE). The motivation for delving into the realm of DVAEs stems from a critical need - the ability to effectively interpret and utilize limited, noisy data. They merge the robustness of DAEs in handling noisy inputs with the generative prowess of VAEs. As highlighted in the research paper “Denoising Criterion for Variational Auto-Encoding Framework”, integrating a denoising criterion into the VAE framework refines the robustness of learned representations, thereby enhancing the model’s generalization ability over various tasks.

VAEs, known for their generative capabilities, introduce noise at the hidden layer level, potentially offering a means to augment limited datasets. On the other hand, DVAEs, an innovative extension of VAEs, introduce perturbation to input data, promising a more robust feature extraction and create additional, realistic augmentations of the data. Our aim here is to comprehensively analyze and contrast the efficacy of VAEs and DVAEs in augmenting such datasets. We hypothesize that while VAEs can offer some level of data enhancement, DVAEs, with their inherent denoising capability, might prove superior in extracting more reliable and robust features from noisy datasets.

Research Problem Statement

The first aspect of this research is to explore the dual functionality of DVAEs — their ability to denoise input data while concurrently learning a generative model of the data distribution. The next aspect is to to compare the performance of DVAEs against traditional VAEs in i) learning robust latent representations, and ii) in downstream classification tasks with richer varied datasets by utilising data augmentation aspect of these generative models.

  1. Learning Robust representation and Generating Synthetic data using DVAEs: Can DVAEs dual capability of denoising input data and learning a generative model of the data distribution simultaneously be exploited to effectively learn robust representations from limited and noisy datasets and utilized to generate additional synthetic data (augmented dataset)? How does it compare to using traditional VAEs?

  2. Performance Enhancement for downstream tasks: How does the DVAE-generated synthetic data impact the performance metrics of downstream classification tasks? Compare performance metrics with traditonal VAE for different noise levels in test datasets.

Methods

Dataset Selection and Preparation

The Fashion-MNIST dataset, which includes 60,000 training images, is selected for the experiments mentioned above. To simulate a limited data environment, a subset of 5,000 images is randomly selected from the dataset. We also create a noisy version of the training dataset to understand the efficacy in scenarios when clean input data is not available.

Figure 1. Sample Fashion-MNIST images

Figure 2. Artificially Corrupted(Noised) Fashion-MNIST images

VAE and DVAE - Architecture and Hyperparameters

The VAE and DVAE architecture is similar and differ only in the sense that DVAE adds noise to input images before passing it to encoder.

The encoder comprises two hidden layers, each with 128 neurons. The input size is flattened to 28 * 28 dimensions. Each hidden layer in the encoder is followed by a ReLU activation function. The encoder’s output is connected to two separate layers: one for generating the mean (µ) and the other for the logarithm of the variance (log-variance), both projecting to a 4-dimensional latent space (z_dims).

On the decoding side, the architecture starts with the latent space and expands through a similar structure of two hidden layers, each with 128 neurons and ReLU activation functions. The final output layer reconstructs the original input size of 28 * 28 dimensions and applies a Sigmoid activation function.

This VAE/DVAE employs a reconstruction loss using the binary cross-entropy between the input and its reconstruction, and a regularization term(KL-Divergence) derived from the latent space to enforce a probabilistic distribution. Each model is trained for 60 epochs with batch size 128.

    input_size = 28 * 28
    z_dims = 4
    num_hidden = 128 
    self.encoder = nn.Sequential(
        nn.Linear(input_size, num_hidden),
        nn.ReLU(),
        nn.Linear(num_hidden, num_hidden),
        nn.ReLU()
    )

    self.mu = nn.Linear(num_hidden, z_dims)
    self.logvar = nn.Linear(num_hidden, z_dims)

    self.decoder = nn.Sequential(
        nn.Linear(z_dims, num_hidden),
        nn.ReLU(),
        nn.Linear(num_hidden, num_hidden),
        nn.ReLU(),
        nn.Linear(num_hidden, input_size),
        nn.Sigmoid(),
    )

Data Augmentation

For augmenting the dataset, we generate 2 newer samples or each input image. First, the image is passed through the encoder part of VAE/DVAE and then sample a latent representation vector around the obtained latent representaion - mean and std.

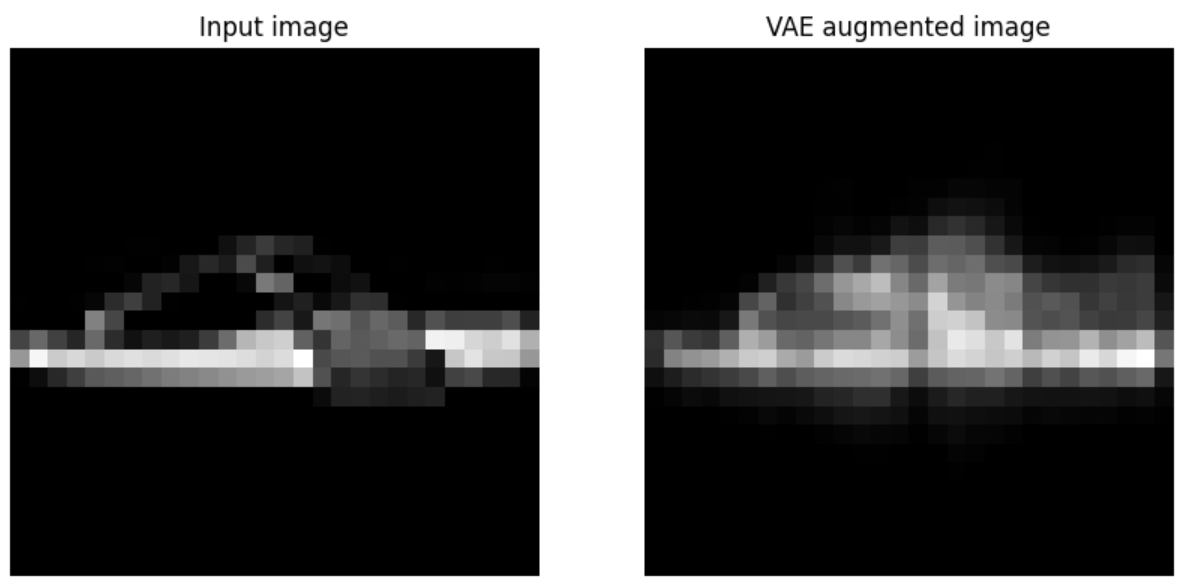
Figure 3. Example: VAE Data Augmentation

Figure 4. Example: DVAE Data Augmentation

Classification Network(CNN) Architecture

The Classification Network(CNN) architecture is comprised of a series of convolutional, activation, pooling, and fully connected layers. Initially, it features a convolutional layer with 1 input channel and 32 output channels, using 3x3 kernels, stride of 1, and padding of 1 with ‘reflect’ mode, followed by an ReLU activation function. This is succeeded by another convolutional layer that increases the depth to 64 filters, maintaining the same kernel size, stride, and padding, accompanied by the same activation function. Subsequently, a max pooling layer with a 2x2 kernel reduces the spatial dimensions of the feature maps, highlighting significant features. The data is then flattened, resulting in a feature vector with a length of 64 * 14 * 14, which feeds into a series of three linear layers, each with 128 units, interspersed with the activation function. This sequence of fully connected layers is designed to capture complex relationships in the data. Finally, the architecture has an output linear layer that maps to the number of outputs (num_outputs=10).

  image_dim = 28
  num_outputs = 10
  act_cls = nn.ReLU
  net = [
      nn.Conv2d(in_channels=1, out_channels=32, kernel_size=3, stride=1, padding=1, padding_mode='reflect'),
      act_cls(),
    ]

  net.extend([
       nn.Conv2d(in_channels=32, out_channels=64, kernel_size=3, stride=1, padding=1, padding_mode='reflect'),
       act_cls(),
       nn.MaxPool2d(kernel_size=2)
    ])
  input_len = int(64 * image_dim/2 * image_dim/2)

  net.extend([
      nn.Flatten(),
      nn.Linear(input_len, 128),
      act_cls(),
      nn.Linear(128, 128),
      act_cls(),
      nn.Linear(128, 128),
      act_cls(),
    ])

  net.extend([nn.Linear(128, num_outputs)])

Results

Here, we utilize the standard Fashion-MNIST dataset for our analysis. Initially, we train the VAE/DVAE network on a subset of 5,000 samples from the training dataset over 60 epochs. Following this, we employ the VAE/DVAE networks to generate synthetic data, leveraging the learned latent space representation for data augmentation purposes. The performance of the augmented datasets is then evaluated using the previously described CNN architecture for classification tasks.

VAE-DVAE Performance

DVAE’s training loss closely tracks the VAE’s loss throughout training. This is interesting because the DVAE is dealing with additional artificial noise, yet it performs on par with the standard VAE. The fact that the DVAE does not exhibit a significantly higher loss than the VAE might suggest that it is effectively denoising the data and learning a robust representation, despite the additional noise.

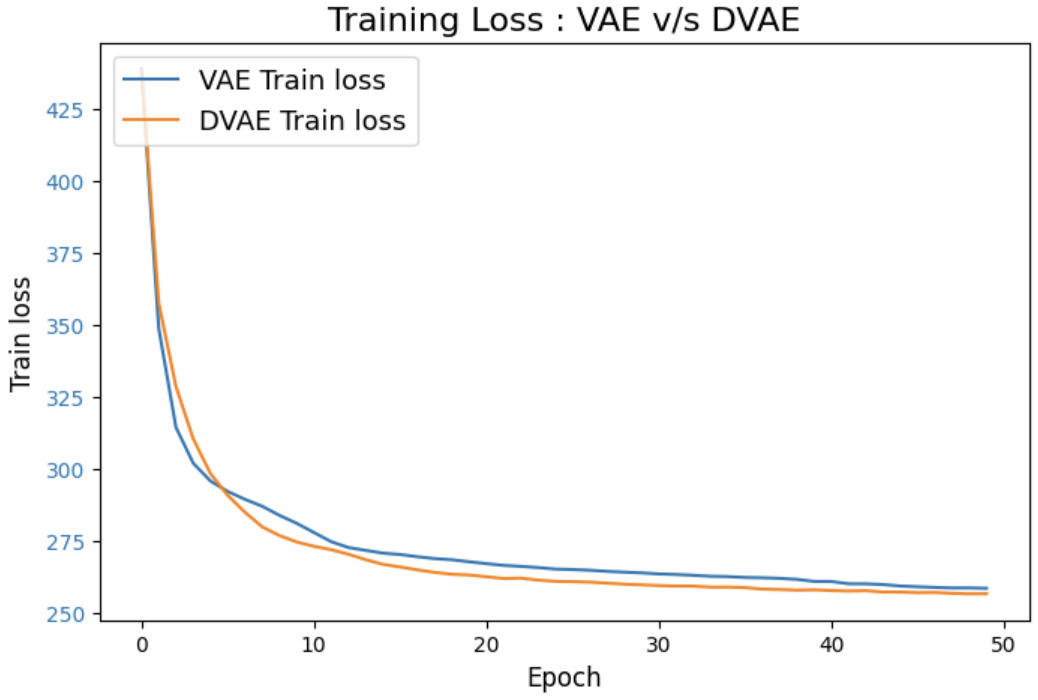
Figure 5. Training Loss: VAE v/s DVAE

Latent Space Visualization

Here, we are visualizing the latent space of VAE and DVAE, a high-dimensional space where each dimension represents certain features learned by the model from the data. For this, we plot a 10x10 grid of images where each image in the grid is generated by the model by varying the values in two chosen latent dimensions (i and j), while keeping the other dimensions set to zero. This helps in understanding the effect of each latent dimension on the generated output.

Figure 6. VAE Latent Space Visualization

Figure 7. DVAE Latent Space Visualization

The lack of visible differences in the latent space structures of both VAE and DVAE indicates that the two models are learning similar representations. To delve into these nuances, we assess the effectiveness of augmented data (created using these learned latent spaces) in a subsequent classification task.

Classification Performance

To delve into the efficacy of VAE and DVAE in augmenting datasets for downstream image classification tasks, we trained a CNN on a limited subset of the Fashion-MNIST dataset to establish a baseline. Subsequently, we generated synthetic data using both VAE and DVAE, aiming to enrich the training dataset and observe the resultant impact on the CNN’s performance. This is crucial considering the initial constraint of limited training data to start with. We used Fashion-MNIST test dataset, which includes 10,000 test images, for evaluating the performance of learned CNN network.

We also tested robustness of these augmented datasets against varying levels of noise (artifically added to test dataset), simulating real-world conditions where test data often includes such imperfections, arising because of the limitations in measurement tools.

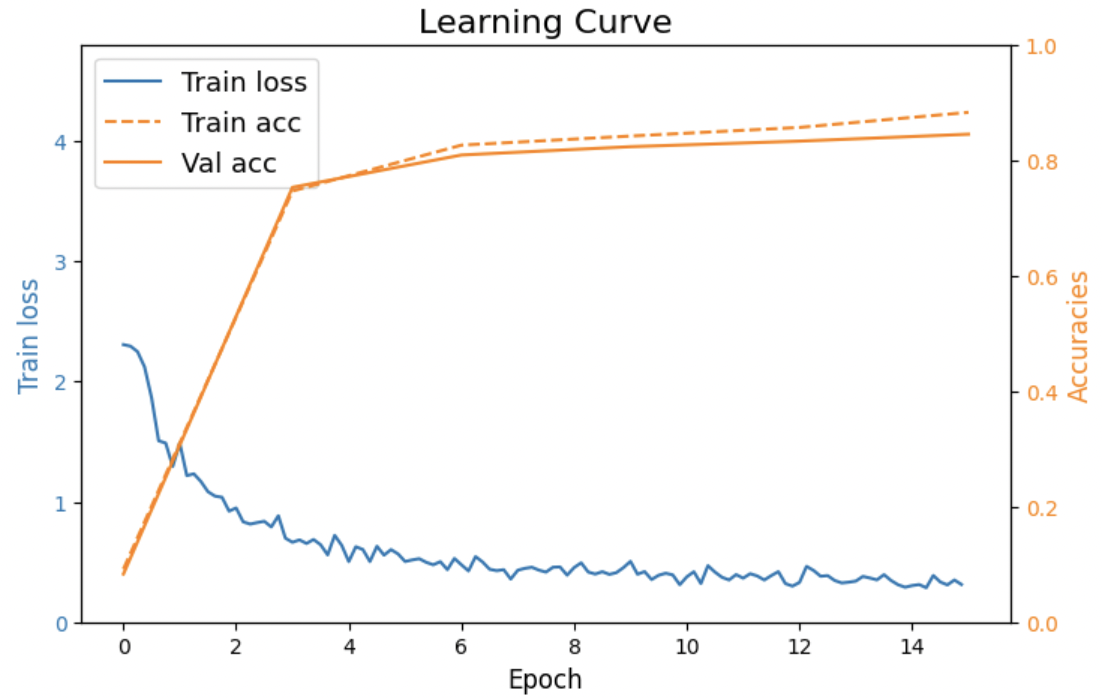
Figure 8. CNN Learning Curve for Limited Dataset

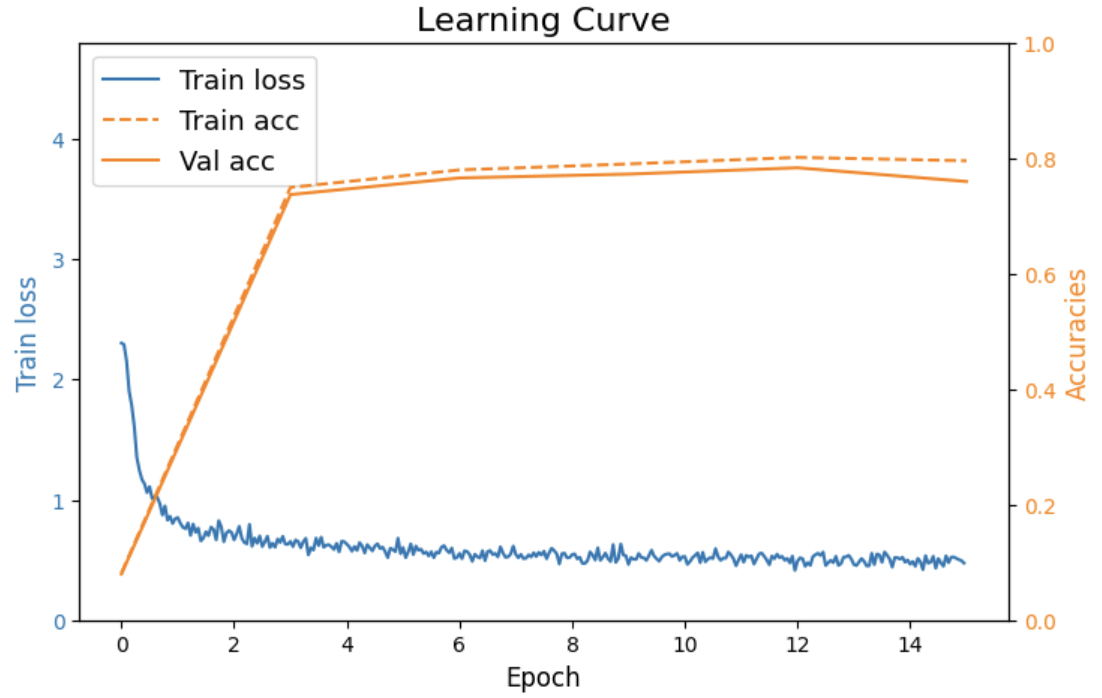
Figure 9. CNN Learning Curve for VAE Augmented Dataset

Figure 10. CNN Learning Curve for DVAE Augmented Dataset

Dataset Type \ Noise Level No Noise 2.5% Noise 5% Noise 7.5% Noise 10% Noise
Limited Dataset 83.56% 83.39% 83.11% 82.33% 81.75%
VAE Augmented Dataset 84.18% 84.03% 83.57% 82.68% 81.43%
DVAE Augmented Dataset 85.32% 84.98% 84.67% 83.98% 82.59%

Artificially corrupted Fashion-MNIST

Here, we deliberately introduced artifical noise to the standard Fashion-MNIST dataset to effectively simulate the real-world scenario where training data is not cleaned and is often noisy and imperfect. Such conditions often pose significant challenges in learning effective representations, making our approach highly relevant for understanding the adaptability and efficiency of VAE and DVAE models in handling noisy data. This way we expose the model and train it on a variety of noise patterns while forcing it to reconstruct the original noised image. The model will learn to effectively separate noise from the signal and will be less likely to overfit to the ‘clean’ aspects of the training data and can thus perform better on unseen, noisy data. This improves the generalization capabilities of the model making it more suitable for practical applications.

Here, we generated synthetic data using both VAE and DVAE which are trained on artifically corrupted Fashion-MNIST dataset. We then compare the performance of CNN network for three datasets - Limited Noisy Dataset with no augmentation, VAE Augmented dataset and DVAE Augmented Dataset, where representations are learned using the noisy training set. Consistent with our earlier methodology, we further evaluated the robustness of CNNs trained with these datasets by testing them against varying levels of noise in the test dataset.

Dataset Type \ Noise Level No Noise 2.5% Noise 5% Noise 7.5% Noise 10% Noise
Limited Noisy Dataset 83.77% 83.79% 83.61% 83.36% 82.98%
VAE Augmented Dataset 85.24% 84.99% 84.62% 84.04% 83.20%
DVAE Augmented Dataset 85.48% 85.38% 85.10% 84.89% 84.58%

Conclusions

Here are the key findings from our research:

  1. Enhanced Learning from Augmented Data: We observed that the CNN trained with data augmented by both VAE and DVAE demonstrated improved accuracy and generalization capabilities, especially when compared to the CNN trained on a limited dataset. This underscores the effectiveness of generative models in enriching training datasets, leading to more robust learning.

  2. Superiority of DVAE in Handling Noise: The CNN trained with DVAE augmented data consistently outperformed the one trained with traditional VAE augmented data in tests involving noisy conditions. This aligns perfectly with our research hypothesis about the dual functionality of DVAEs — not only do they learn a generative model of the data distribution but also excel in denoising input data.

  3. Robustness to Varied Noise Levels: A crucial aspect of our research was evaluating the performance of augmented datasets under various noise levels. The augmented datasets, especially those generated by DVAEs, maintained consistent performance across different noise conditions. This suggests that the models have not only learned the essential features of the data but are also adept at filtering out noise.

In downstream classification tasks, DVAE-generated synthetic data improved performance metrics, surpassing those achieved with traditional VAE-generated data, particularly in tests with varied noise levels. This validates our hypothesis and highlights the potential of DVAEs in real-world applications where data is limited and data quality is a critical factor.

The next steps for this research could be to focus on expanding the types of noise tested in our experiments to evaluate the adaptability and robustness of DVAEs in a broader range of real-world scenarios. We could conduct more comprehensive data augmentation experiments to delve deeper into the capabilities of DVAEs in enhancing neural network learning and generalization.