Regularization Techniques for Attention Layers in Transformer Models
Attention layers are an integral part of the success of transformer models, but can also lead to overfitting on parts of input data when there is limited training data. Therefore, researchers have proposed methods to regularize attention layers to reduce overfitting and increase generalizability. This blog will analyze popular methods and explore novel approaches to regularization in attention layers.
Introduction
Transformer models are exceptionally popular and successful at completing many tasks. However, they can overfit to their training data if they are not given enough data to generalize. Frequently, part of the reason for overfitting is the overfitting of a self-attention layer, which highlights important tensors in the model. However, if there is not enough data, the attention layer can overfit to the training data and highlight some tensors too much. Therefore, researchers have proposed methods of regularizing attention layers. Adding regularization can be complex and there have been many different approaches to solving this issue, from simply smoothing attention layers to encouraging multi-headed models to approach different solutions. Therefore, there are differences in the effects of different regularization methods and some might perform better in different circumstances. There does not seem to be a standard approach to dealing with this form of regularization and while many authors have claimed their regularizations have positive effects on training, there are few comparisons of regularization methods. In this study, we will analyze previous work on regularizing self-attention layers and propose new regularization techniques to identify the advantages and disadvantages of differing models.
Background
There are many proposed regularization strategies for self-attention layers. We implement and utilize many of the more popular strategies in this study while also drawing inspiration from other methods in proposed methodologies. However, we could not find comparisons across regularization methods or implementations of these methods publicly available. Therefore, we implemented previously proposed strategies and proposed new regularization strategies based on methods seen in fully connected neural networks. The methods used fall into the following three categories. We will explain the exact methods and implementations used for each of these three categories in the methodology section. They represent a solid overview of the self-attention regularization space and contain the most popular methods currently in use.
Dropout Based Methods
Dropout based methods involve randomly setting a specified fraction of the input units to zero during training time, which helps in preventing overfitting
Weight Smoothing Methods
Weight smoothing methods aim to regularize the self-attention layer by modifying the weights such that the attention weight are closer to the uniform distribution and do not overly emphasis specific inputs. This helps prevent overfitting by not allowing the model to only use a few inputs
Cross Head Methods
Cross head methods involve techniques that operate across different attention heads, aiming to diversify the learned representations and prevent redundancy
Methodology
Overall Architecture
We begin by implementing and benchmarking a vision transformer with no regularization. We had previously implemented a transformer model as part of 6.s898 problem set 3, so we used this as basis for our models. This model follows an architecture stemming from An Image Is Worth 16X16 Words
- Take an image and split it into patches of specified size.
- Embed these patches and add a positional encoding to their embedding.
- Treat these embeddings as a sequence input to a transformer model.
- Use a transformer model with multi-head self-attention to transform the input into some specified space.
- Use this output to classify the image.
For this specific model, we use a 6 layer transformer with 5 self-attention heads and a patch size of 4. We will be focusing on the multi-head self-attention phase of the transformer model. The following is a diagram of the overall architecture of a vision transformer.
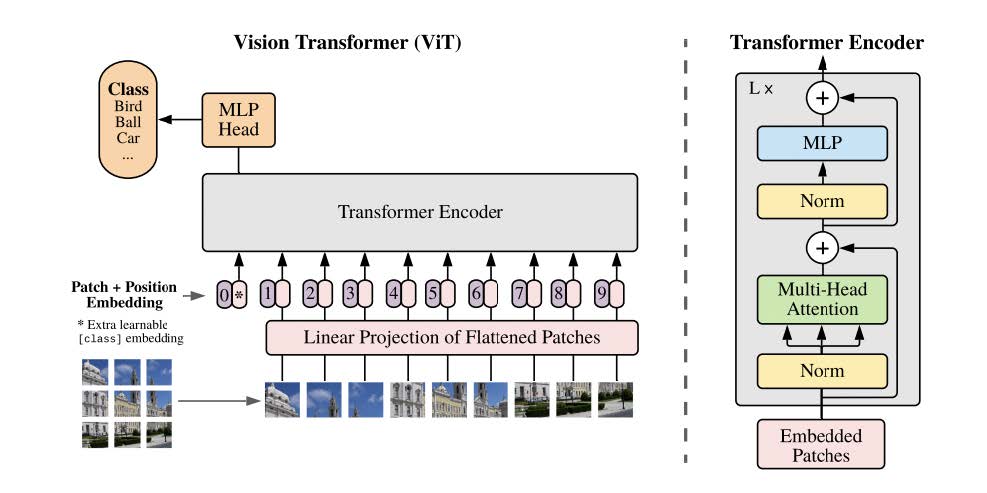
Data
We use the CIFAR-10 and CIFAR-100 datasets for this study

Regularization Methods
We tested the following regularization methods for our model. We tested models contained within the three different categories of regularization mentioned in the background above, these being dropout based methods, weight smoothing methods, and cross-head methods.
Dropout Based Methods
DropColumn
This method uses dropout, a common regularization method used in fully connected neural networks, in self-attention layers. This can force the model to generalize better and not rely on specific inputs as much. The authors propose the following methodology to add dropout to the model, which is similar to standard dropout techniques in neural networks. To perform dropout, each column in the attention weight matrix is sampled from a Bernoulli distribution with some probability. We use a dropout ratio of 0.2 for these experiments. We set the sampled columns to zero weight during training. Therefore, we are able to randomly drop columns in the attention weight matrix.
DropHead
We can also perform dropout on the heads across the multi-head attention layer. With this method, we completely drop heads during training to reduce reliance on particular heads and increase the generalizability of the model. We use a dropout ratio of 0.2 for these experiments. This prevents the model from being dominated by a few attention heads.
Weight Smoothing Methods
Relaxed Attention
This method smooths the attention weights in the self-attention layer to reduce overfitting. This helps reduce the magnitude of the highest attention scores. We do this by mixing in the uniform distribution to attention weights during training. We use some parameter $ \color{white} \gamma $ to evaluate different levels of mixing. Therefore, we apply the following function to our self-attention weights.
$ \color{white} A[i,j] = (1-\gamma) \times A[i,j] + \gamma \times \frac{1}{T}, \quad \forall i, j \in [0,1,…,T]$
We use $ \color{white} \gamma = 0.1 $ for our experiments. This adds a low level of uniformity but prevents the model from only attending upon a small number of tensors during training. Therefore, this should limit the amount of overfitting that is possible.
Noise Injection
Noise injection has been used to regularize fully connected neural networks, but we have not found any literature that proposes using noise injection to regularize self-attention layers. We propose two methodologies to add regularization and robustness to our model training. We inject noise into our input embeddings with the following formula.
$ \color{white} x_{i,j}^{noised} = x_{i,j}+ \frac{1}{100} * median(x) * N(0,1) $
-
Overall Noise Injection: The first methodology involves simply adding noise to the input during training. We do this by adding Guassian random noise to the input before calculating self-attention weights in each layer of the transformer.
-
Individual Head Noise Injection: Our second proposed methodology takes advantage of the multi-headed transformer design. We add different Gaussian random noise to each head, such that the heads will receive different inputs. Therefore, the model must become more robust to different inputs.
Cross-Head Methods
Decorrelation
We propose adding a decorrelation term to our loss function. The goal of this loss is the reward differences across attention heads. We begin by calculating the self-attention weights for all of the attention heads. We then compute the pairwise dot products of each head’s attention weights. This will increase the loss if there are heads that are highly correlated. This will cause the heads of the network to differ from the other heads in the network and hopefully generalize better. Therefore, we use the following loss term.
$ \color{white} \text{Added Loss} = \sum_{i={0,…,H},j={i+1,…,H}} \frac{\text{sum}((\Lambda_i^T \Lambda_j)^2)}{\text{Number of elements in }\Lambda_i^T \Lambda_j}$, where H is the number of heads and $ \color{white} \Lambda_i$ is the ith attention head weights.
This method is inspired by another method, multi-head attention with disagreement regularization
Normalization
We propose adding the 2-norm of all elements in the attention weight matrix to the loss function to limit the emphasis of individual inputs. Therefore, this will smooth the weights and reward more uniform predictions. This should reduce overfitting and make the model more generalizable. We calculate this norm using $ \color{white} \frac{\text{torch.linalg.norm(attention weights)}}{\text{number of elements in attention weights}} $. This computes the 2-norm of all elements across attention heads and adds more loss to weights that emphasize specific inputs more than others. Therefore, this should add smoothing to the weights.
Training
We train each model for 25 epochs on the full training set with a batch size of 256. We use the AdamW optimizer, with a learning rate of 0.001. We use the following parameters for our vision transformer.
| Parameter | n_channels | nout | img_size | patch_size | dim | attn_dim | mlp_dim | num_heads | num_layers |
|---|---|---|---|---|---|---|---|---|---|
| CIFAR-10 | 3 | 10 | 32 | 4 | 128 | 64 | 128 | 5 | 6 |
| CIFAR-100 | 3 | 100 | 32 | 4 | 128 | 64 | 128 | 5 | 6 |
We train each model individually on both datasets.
Results
CIFAR-10
We begin by analyzing the training results on the CIFAR-10 dataset.
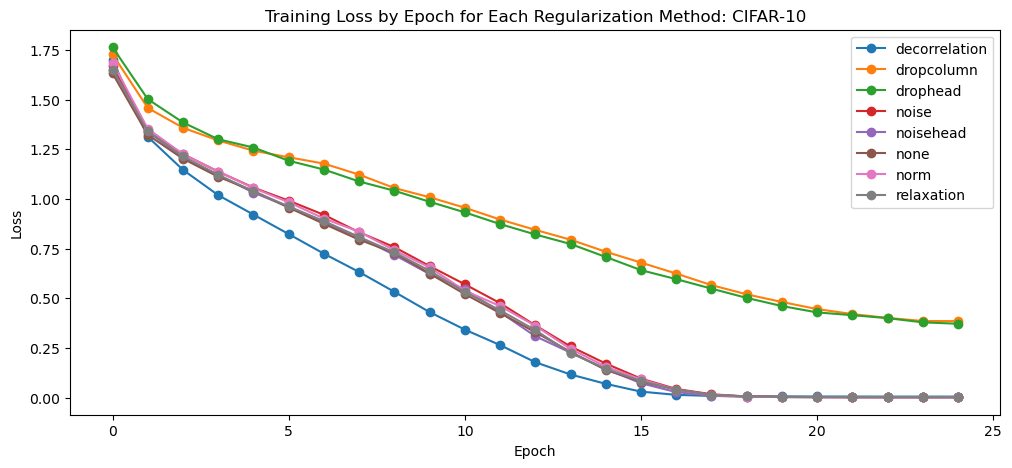
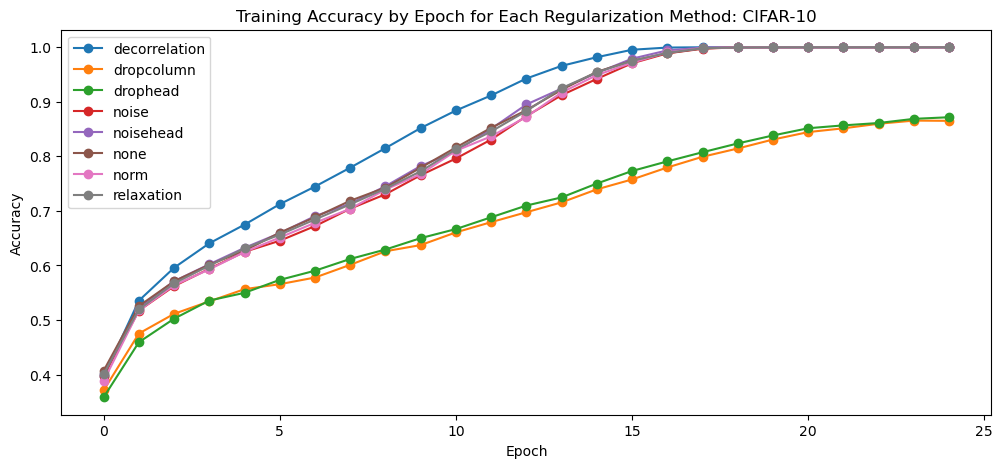
We see that most of the models, except for the dropout based models, achieve near zero error and perfect accuracy on the test set. Therefore, we see that the dropout term is stopping the model from perfectly memorizing the dataset but all other regularization techniques are not forcing the model to change the weights enough to prevent perfect accuracy.
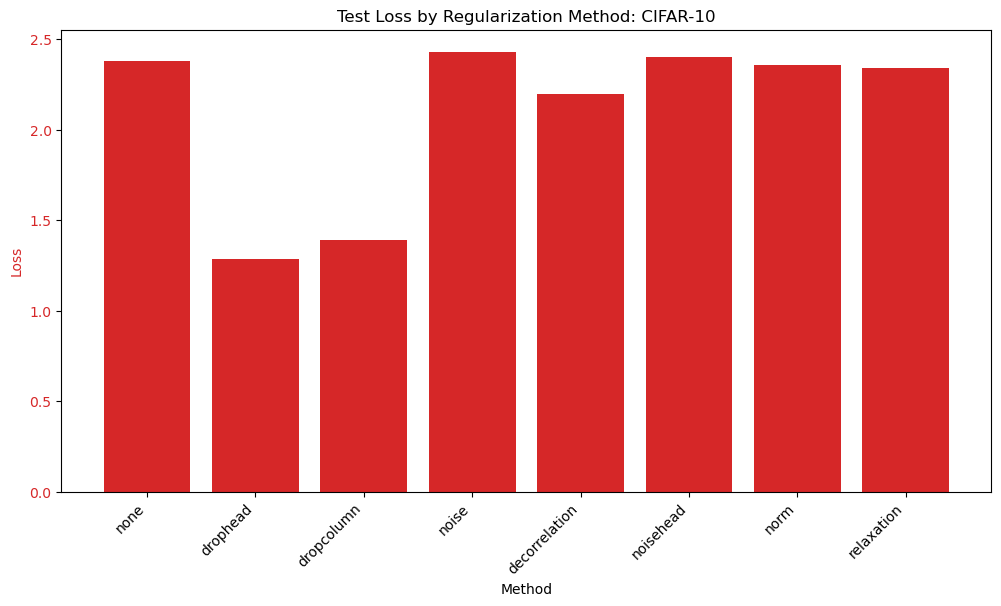
Looking at the test results, the two dropout models have much lower loss achieved on the test dataset. The rest of the models have similar losses on the test dataset.
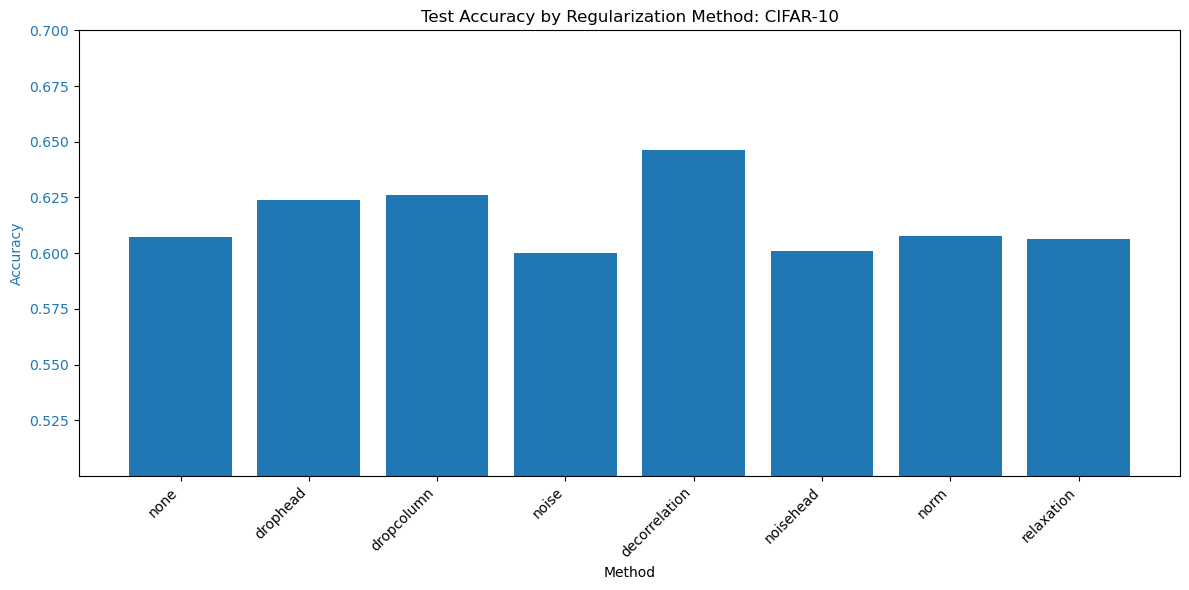
We see that the two dropout methods also have higher accuracy than the model without regularization. However, the decorrelation model has the highest test accuracy. Overall, the test dataset results are significantly lower than state of the art and a more advanced model may be needed to achieve better performance.
CIFAR-100
We move on to training and testing the models on the CIFAR-100 dataset. This dataset has more classes and therefore fewer examples of each class. Therefore, the model finds it more difficult to generalize on the test dataset.
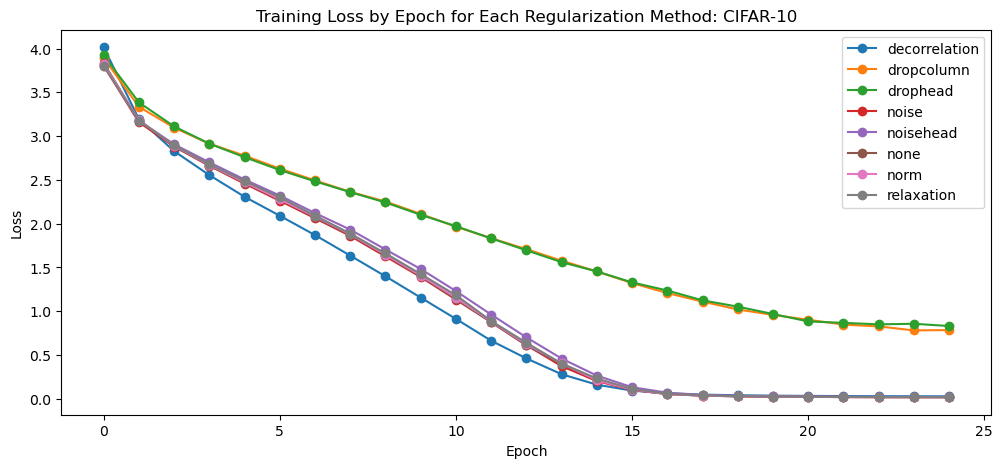
Again, we see that all methods except the dropout based methods achieve near-zero error.
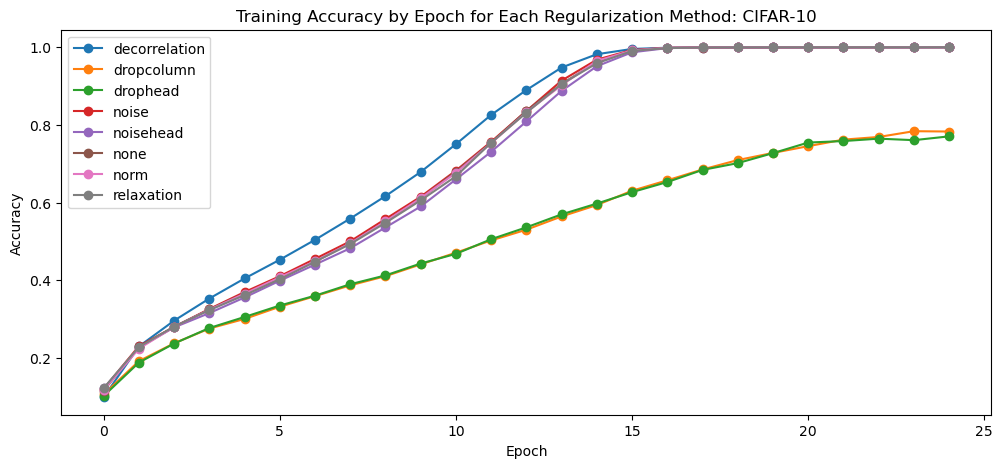
We see similar results to the CIFAR-10 dataset in training. The two dropout methods are unable to achieve perfect loss and accuracy but all other methods are able to. This includes the methods with added loss, that being the normalization method and the decorrelation method. This will depend on the parameters of the model and these models would have higher loss if we used more emphasis on the added loss.
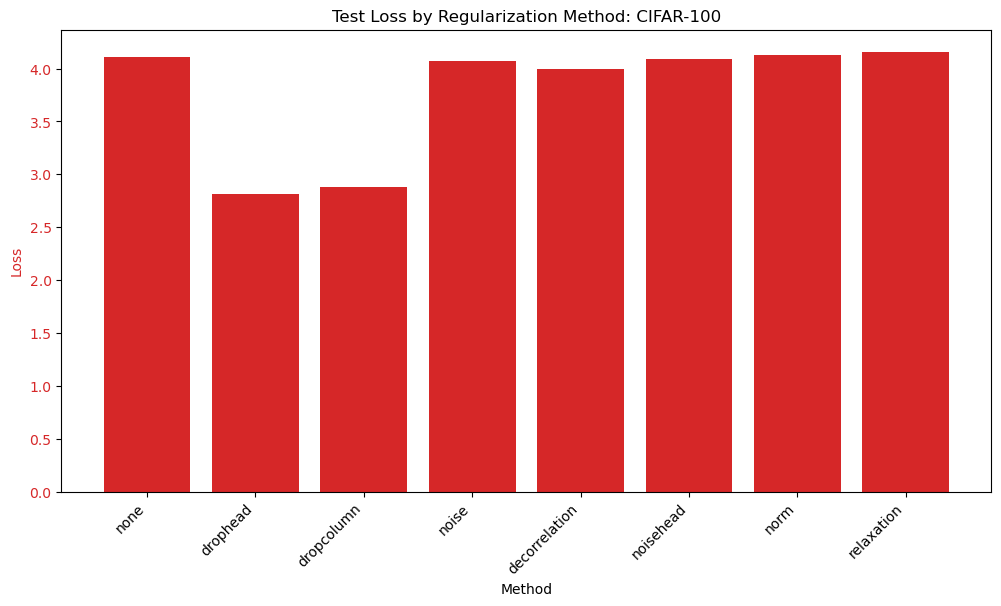
We see that the two dropout methods have significantly lower loss on the test dataset, with all other methods performing similarly.
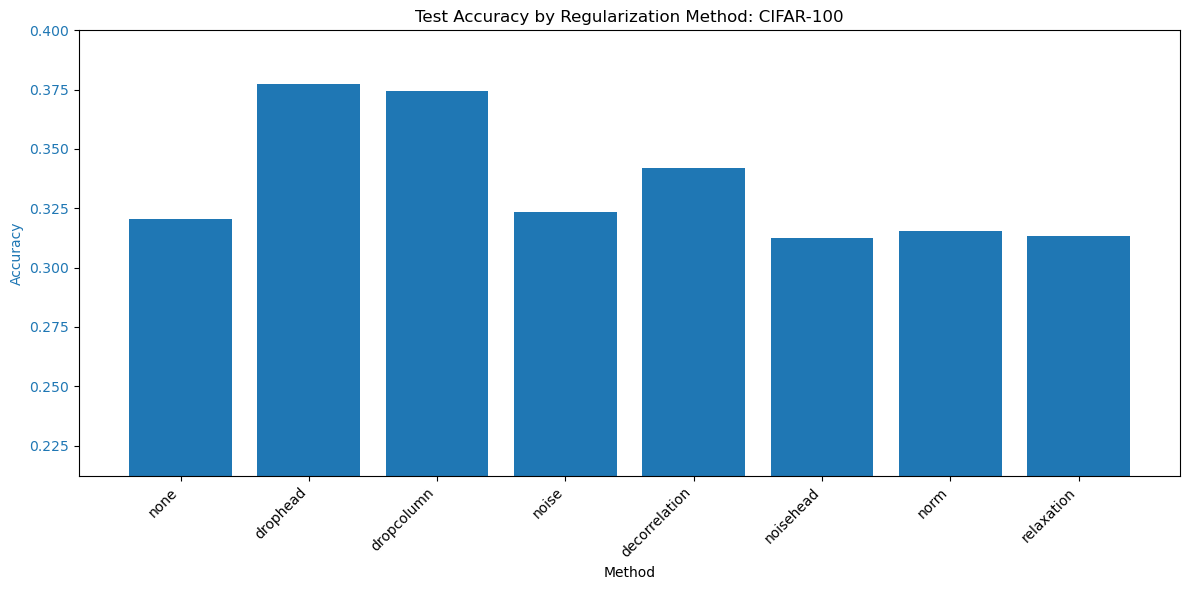
We again see consistent results with the CIFAR-10 dataset. The two dropout methods and decorrelation improve the accuracy on the test set, while the others are about the same as without normalization. In this case, the drophead method performs the best.
Further Research
Further research is needed to further improve the generalizability of this transformer architecture for these datasets. The model still has overfitting issues, even with high regularization and so more research with different architectures or regularization methods is needed to improve the study. Further comparison of regularization methods on alternative datasets and types of data, such as text, would also be valuable to look at.
Conclusion
Regularization is an important tool to reduce overfitting and improve the generalizability of a model. The results show that adding various forms of regularization can improve the results of a model, but our implementations did not cause dramatic change to the ability of the model to generalize to the test set. Most of the models still had a very large gap between their training accuracy and test accuracy. However, we did see notable improvements for both the dropout models and the decorrelation model. The dropout models were the only models that added regularization such that the model could not perfectly memorize the training set. Therefore, their training accuracy was significantly lower but they also had higher test accuracy. Additionally, the decorrelation model was also successful. While the model followed a similar pattern during training to the model without regularization, the test accuracy was generally higher, suggesting the added error did force the model to learn different parameters. Therefore, based on these results, adding regularization can be helpful in improving the generalizability of transformer models, especially when they have limited data. The other methods, such as the noise based methods, normalization, and relaxation did not appear to have a significant effect on training or test outputs. It is likely that alternative parameters or architectures are needed to realize their effect. Lastly, while this analysis was only completed using vision transformers, different datasets or network architectures may have significantly different results. Therefore, these other regularization methods may be more successful in other contexts. However, these tests prove that there are circumstances in which regularization can have a beneficial effect on transformer performance and is therefore a worthwhile experiment when dealing with overfitting transformers.