Injecting Node Information via Embedding Initializations
Graph Neural Networks (GNNs) have revolutionized our approach to complex data structures, enabling a deeper understanding of relationships and patterns that traditional neural networks might miss. This project looks into the potential of embedding initializations in GNNs, particularly in the context of molecular function prediction and protein retrieval tasks. By investigating the effect of intentional, information-rich initializations versus random initializations, we aim to enhance the learning efficiency and accuracy of GNNs in these domains. Our study focuses on a precision medicine knowledge graph (PrimeKG) and employs TxGNN, a GNN model initially designed for disease-drug link prediction, repurposed for protein-molecular function link prediction. We explore the impact of using ESM embeddings for protein nodes, hypothesizing that these embeddings could provide structural information not explicitly present in the graph data. Through comparisons of the latent spaces and performances, we look to see the effectiveness of these embeddings in improving the model's predictive powe of protein function.
Introduction
Graph Neural Networks (GNNs) have emerged as a transformative tool in machine learning, with the ability to capture the complex structures and relationships inherent in data. In molecular property prediction, for example, GNNs are great at encoding the atomic structure and intermolecular forces into high-dimensional embeddings, leading to more accurate predictions of chemical properties and drug efficacy. GNNs have also be used in traffic time prediction problems, physics simulations and social media analysis applications. Through message-passing and updating, GNNs are capable of learning embeddings that encode informations of node neighbors and long-distance complex connections – that we, as humans, may not be able to make. The quality of the embeddings is not only important for the accuracy of the task the GNN is trained on, but quality node embeddings can be used through transfer learning – enabling models trained on one task to adapt and excel in another. The importance of good embeddings in GNNs is why we want to look closer at embedding initializations and if we can inject additional information – not present in the graph – to result in better learned embeddings after training.
Possible applications of initial embedding initializations could help in the field of drug discovery. For GNNs used for protein retrieval trained on a biomedical knowledge graph, using ESM embeddings for the proteins could add structure information that is not previously encoded in the graph entities.
Project Outline
We will explore the question can additional node information be injected into the model by using intentional embedding initializations rather than random initializations? Furthermore, are the learned embeddings better representations of the nodes? To answer this question we will follow the steps outlined below:
- We will download a precision medicine knowledge graph that and use a GNN, TxGNN, that is implemented for disease-drug link prediction on a biomedical knowledge graph as a baseline model.
- We will modify the GNN for protein-molecular function link prediction.
- Generate and download ESM embeddings for each protein
- Pretrain and finetune two models – one using random protein node initialization and one using ESM embeddings for protein node initialization. We must pretrain our own models, rather than use the already pretrained model, since we are focusing on how different node initializations impact the predictive power.
- Evaluate both models
- Visualize latent spaces before pretrain, after pretraining and after finetuning
Related Work & Motivation
In reviewing the literature, we found several papers which reference the possibility of improved performance through a more informed initialization process. As discussed by Li et al., the initialization methods used for GNNs, such as Xavier random initialization were originally designed for CNNs and FNNs. In that setting, the Xavier approach helped to avoid vanishing gradients and maintain a constant information flux. However, Li et al. point out that by leveraging the structure of the graph, we can likely do better than the random intializations used previously
In the paper detailing TxGNN, Huang et al. present promising results on their ability to predict drug repurposing opportunities using a GNN
Previous work by Cui et al. has explored the power of artificial node initializations, finding that encoding structural and positional information in the node initializations can have profound effect on the ability of a GNN to accurately predict features based on the graph. They provide a basis for our investigation by showing the effect that initializations can have on the results, if done correctly. We seek to build on this work by testing the effect of injecting related, but not exactly equivalent information through the node initializations
Not only did we see an opportunity to try a different initialization method, but this problem also lent itself well to data-informed initializations. The molecules in TxGNN have a wealth of knowledge about them which is not represented in the linkages in the graph, some of which is represented in the ESM embeddings of the molecules. Thus, we thought that by supplying these embeddings to the GNN, we might be able to leverage the additional data to make better predictions.
Data
We used a precision medicine knowledge graph (PrimeKG) constructed by Marinka Zitnik’s group at Harvard
The other data used were ESM embeddings for proteins in PrimeKG. ESM embeddings, or Evolutionary Scale Modeling embeddings, are high-dimensional vector representations of proteins, derived from advanced machine learning models developed by Meta trained on large datasets of protein sequences. These embeddings capture the intricate structural and functional characteristics of proteins, reflecting evolutionary relationships and biochemical properties that are crucial for various biological and computational applications
GNN
The model we used as a baseline is TxGNN, a graph neural network trained on PrimeKG used to make therapeutic drug predictions for diseases
Architecture
The GNN has two linear layers with parameters n_input, n_hidden, and n_output. For all our models n_input is 1280, restricted by the length of ESM embeddings. We play around with different dimensions for the hidden and output layers. Leaky ReLU activation is used after the first layer.
Training
The first step of the training phase is node embedding initialization. The default, which is our random control, is to initialize all nodes using Xavier uniform initialization
During the training phase, the GNN uses a standard message-passing algorithm to update and optimize the node embeddings. There is a relation-type specific weight matrix (for each of the 29 relation types) used to calculate relation-type specific messages. The message for one relation to the some node $i$ is calculated using this equation: \begin{equation} m_{r, i}^{(l)} = W_{r, M}^{(l)} h_i^{(l-1)} \end{equation}
For each node $v_i$, we aggregate incoming messages from neighboring nodes for each relation-type $r$, denoted as $N_r(i)$. This is done by taking the average of these messages: \begin{equation} m_{g_r, i}^{(l)} = \frac{1}{|N_r(i)|} \sum_{j \in N_r(i)} m_{r, j}^{(l)} \end{equation}
The new node embedding is then updated by combining the node embedding from the last layer and the aggregated messages from all relations: \begin{equation} h_i^{(l)} = h_i^{(l-1)} + \sum_{r \in TR} m_{g_r, i}^{(l)} \end{equation}
Finally, DistMult
Model Evaluation
We fixed all parameters and hyperparameters, and trained two models – one using random initializations and one using ESM embeddings. We pretrained for 3 epochs with a learning rate of $1e-3$ and a batch size of 1024. We then finetuned for 150 epochs with a learning rate of $5e-4$.
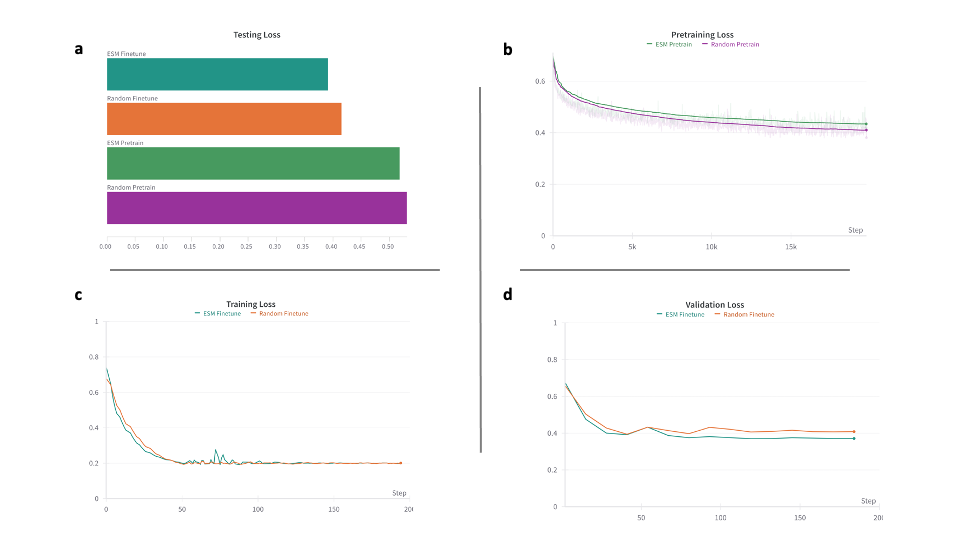
These results are promising and using ESM embeddings to initialize the protein node representations slightly improves the model. The ESM model has a final testing loss of 0.3915, whereas the random model has a final testing loss of 0.4151. However, the difference between the models is slim and may not be significant, especially looking at the similarities in the pretraining, training and validation loss curves. Later, we will look more in depth about how the embedding spaces vary between the 2 models which has the potential to yield more interesting results.
Testing varying hidden and output layer dimensions
We wanted to see the impact changing the hidden and output layer dimensions would have on model performance. We tested 3 models, with parameters detailed in Table 1. All models outside of this experiment, unless otherwise specified, have the same parameters as Model 1.
| Input Dimensions | Hidden Layer Dim. | Output Layer Dim. | |
|---|---|---|---|
| Model 1 | 1280 | 1280 | 1280 |
| Model 2 | 1280 | 512 | 512 |
| Model 3 | 1280 | 512 | 128 |
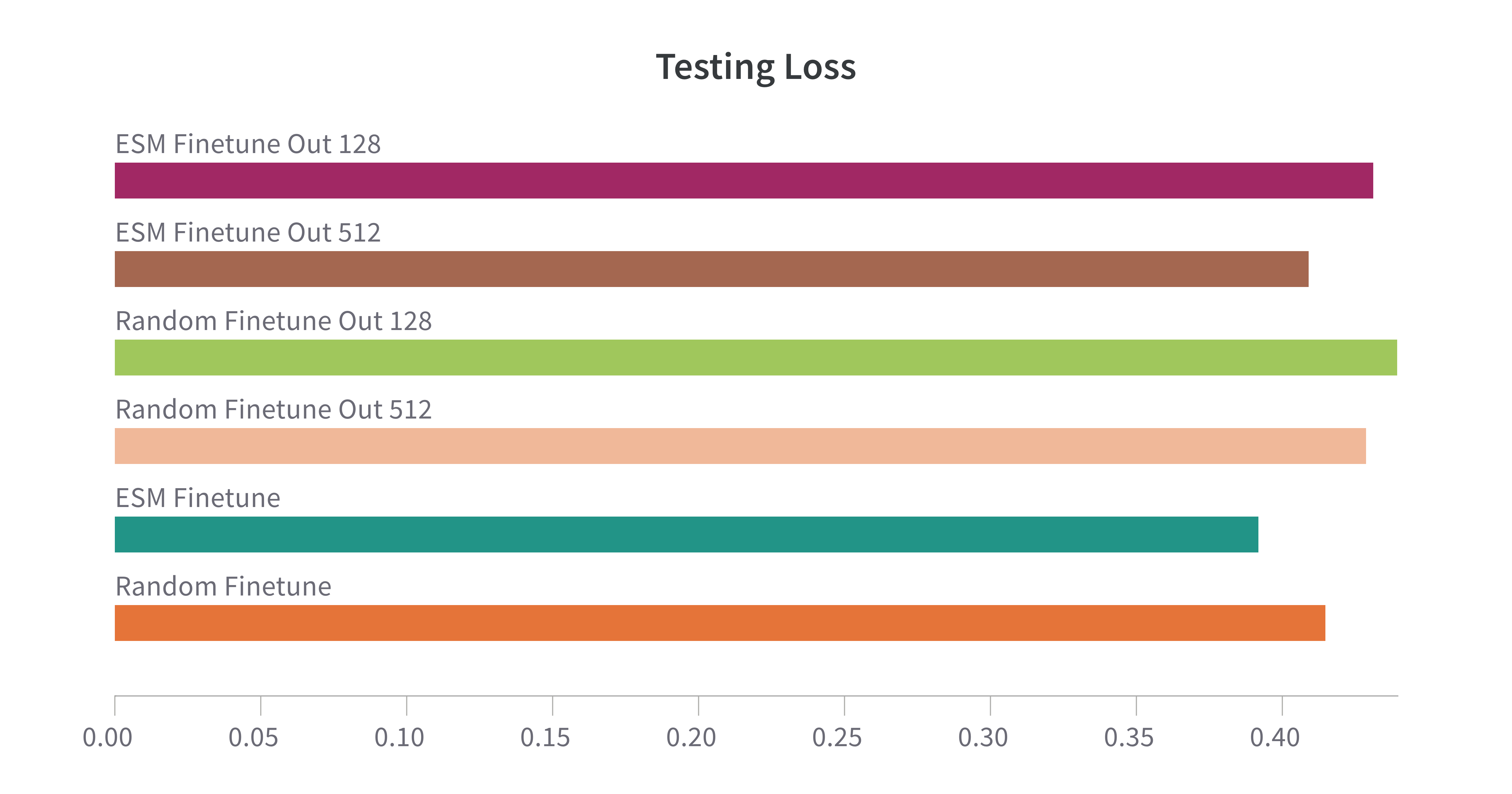
We can see from the testing loss that when just comparing ESM initialized model, testing loss increases as the output layer decreases. The same trend holds true between random initialized models. We can also see that when comparing ESM and random models for the same layer dimensions, ESM always slightly outperforms the random model.
Latent Space Visualizations
In the fast-evolving world of deep learning, the analysis of model latent spaces has emerged as an interesting area of study, especially to get a better understanding of how models are achieving their tasks. These spaces are important to understanding how complex models like GNNs perceive and process the intricate relationships and structures inherent in graph data. GNNs can learn powerful representations that capture both node-level and graph-level features. By analyzing the latent spaces of GNNs, we can get insights into how these models prioritize various patterns and connections within the data. The following analyses visualize the latent spaces our models, clustered and colored in different ways, to get a deeper understanding of how the ESM initialized embeddings are effecting the GNN.
We first were curious whether, after training our model, the final embeddings retained structural information about the proteins. To do this, we first clustered the original ESM embeddings using K-Means clustering. Next, we visualized the embedding space of the original ESM embeddings, the final embeddings from the ESM model and the final embeddings from the random model using t-distributed Stochastic Neighbor Embedding (t-SNE) for dimensionality reduction. From the t-SNE plot of original ESM embeddings, we can clearly see the clusters from K-Means which serves as a verification of our clustering technique.
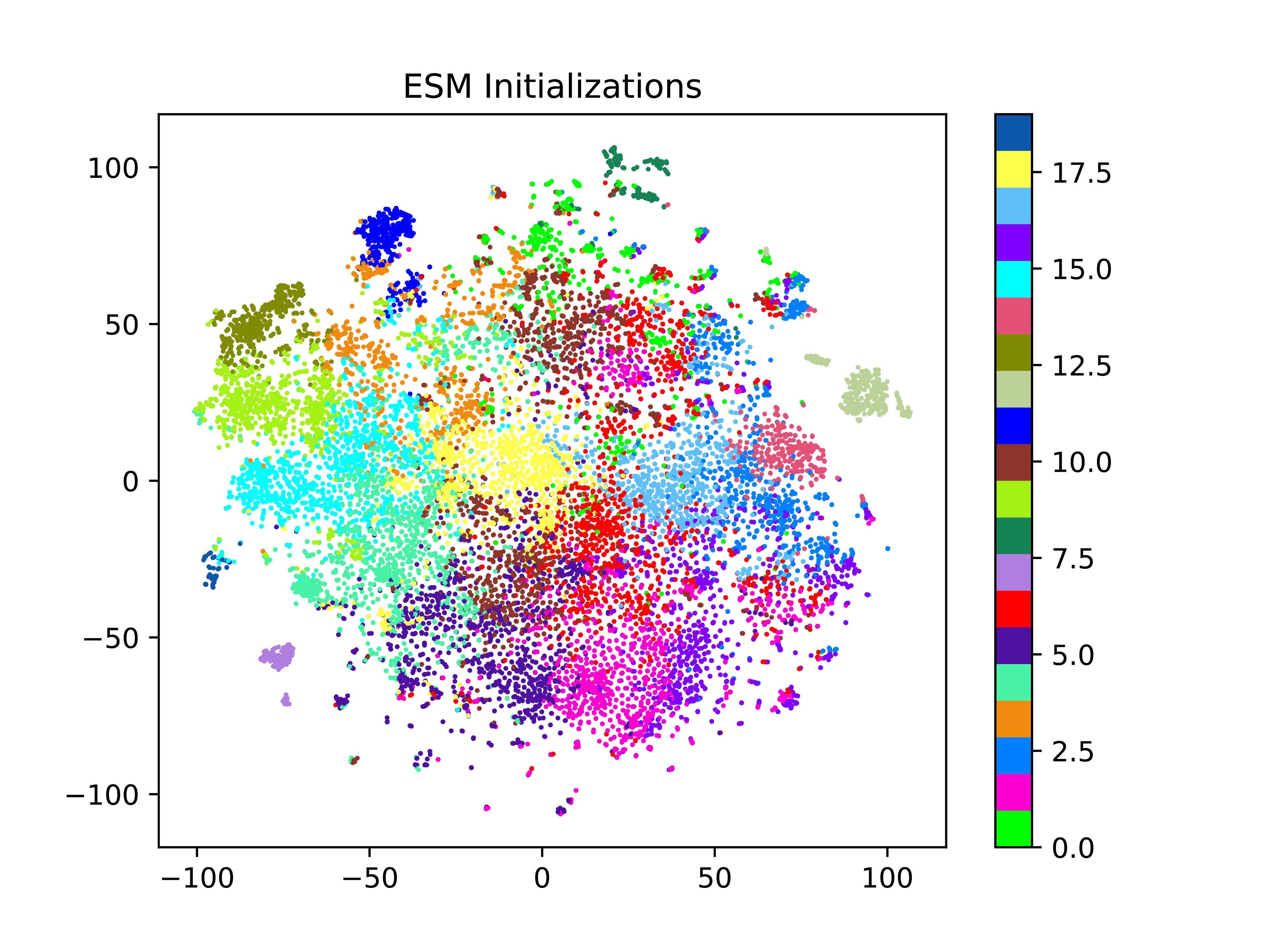
Looking at the embedding space for the ESM and random models, colored by ESM clusters, we note that most of the ESM structural information (used to create the clusters) seems to be forgotten during the training process, as evidenced by the mostly random assortment of colors present in the t-SNE plot. We note that some clusters do remain, for example cluster 12 (light sage green on the right side of the ESM initialized plots) is still clustering in the final embeddings (top middle cluster). However, the most prominent ones appear in both the ESM initialized and random initialized data, meaning that the ESM embedding did encode some function, but the model using random initialized embeddings was able to capture that relation as well.
Given that the final embedding space for the ESM model didn’t seem to retain much of the information for the ESM embedding initialization, we were curious whether the ESM and random embeddings converged to a similar space. To test this theory, we clustered the final ESM model embeddings and subsequently visualized the final embeddings of the ESM and random models using t-SNE and colored by those clusters.
If the two models converged to similar embedding spaces, we’d expect to see that clusters found in one embedding space would also be found in the other. This is the case, as seen in the two plots below. Both plots are colored based on a clustering of the final embeddings generated by the ESM initialized network, and they share many of the same structures, indicating that the two networks were able to pick up on mostly the same features in the underlying information. Both models converged to a similar embedding space different initialization methods.
Testing varying hidden and output layer dimensions
As mentioned earlier, we tested different dimensions for the hidden and output layers to see whether more and less output dimensions would retain the original ESM embedding information.
Although there are more distinct clusters on the t-SNE plots as the number of output dimensions increases, these clusters are not the same as the clusters from the original ESM embeddings (seen by the randomly colored dots). Therefore, neither of these 3 models retained the structural information provided by initializing with ESM embeddings. It does not seem that decreasing output and hidden layer dimensions improves the model performance or latent space of our GNN.
Clustering by molecular function labels
Because our model’s task was to predict links between protein and molecular function nodes, we were curious to see if the final embeddings for the protein nodes would cluster well on the function labels. However, this wasn’t as straight forward as having 1 molecular function label for each protein node, because each protein may be linked to multiple molecular functions. One protein may have multiple molecular function Gene Ontology (GO) annotations because the GO database uses a hierarchical system to categorize functions, where broader functions encompass more specific ones. A protein can be involved in several distinct biochemical activities, each represented by its own GO term, reflecting the diverse roles a protein can play in the cell. Instead of a single label, we extracted a molecular function profile, $v_i$, for each protein where $v_i[j] = 1$ if a link exists between protein $i$ and function $j$. We then had a sparse matrix, $V^{i \times j}$. Before clustering, we performed dimensionality reduction using truncated SVD which is optimal for sparse matrices. Finally, we performed K-Means clustering.
Looking at the t-SNE plots, there is no apparent clustering by molecular function profiles in the final embedding spaces for either the ESM model or the randomly initialized model. There are multiple possible explanations for this. One explanation is that the actual objective is to prediction each singular link between a protein and a function node, not to predict do well at predict all function nodes linked to a protein at once. On top of that our GNN uses self-supervised learning, therefore the molecular function profiles are not true labels used during training.
The second plausible explanation has to do once again with the hierarchical nature of molecular function GO annotations. Because the molecular function nodes have random indices when stored in PrimeKG, it is not apparent that molecular function that have the same parent function are close to each other, or their parent function in the molecular function profiles. Therefore, when performing truncated SVD and subsequently k-means clustering, the similar functions may not be clustered together if their indices are far apart. Further analysis could be done to reorder the molecular function nodes and then conduct hierarchical clustering, instead than k-means. These possible clusters may then be found in the final latent spaces for the two models.
Discussion
In this post, we have modified and fine-tuned a Graph Neural Network, TxGNN originally designed for drug-repurposing prediction, for protein function prediction with a variety of initializations of the node embeddings. We observed that while much of the information in the initialization is forgotten during the training process, a small amount is retained, leading to slightly better performance on the test set in the final network. This provides a potential avenue for further study, investigating the overall effects of informed initialization techniques on GNN performance. Some of this investigation is discussed in Li et al.