Recurrent Recommender System with Incentivized Search

This project considers the use of Recurrent Neural Networks (RNNs) in session-based recommender systems. We input sequences of customers' behavior, such as browsing history, to predict which product they're most likely to buy next. Our model improves upon this by taking into account how previous recommendations influence subsequent search behavior, which then serves as our training data. Our approach introduces a multi-task RNN that not only aims to recommend products with the highest likelihood of purchase but also those that are likely to encourage further customer searches. This additional search activity can enrich our training data, ultimately boosting the model's long-term performance.

Introduction

Numerous deep learning based recommender systems have been proposed recently . Especially, the sequential structure of session or click-logs are highly suitable for the inductive biases provided by recurrent/convolutional neural networks . In such setting, the input of the network is a sequence of consumers’ search behavior, while the output is the predicted preference of the items, i.e. the likelihood of being the next in the session for each item. The ultimate goal is to pinpoint the optimal product for the consumer, thereby increasing sales. An example of where this could be applied is the “featured product” on platforms like Amazon.

However, a challenge with this model is the sparsity of data. It’s well-known that the products in retail has the “long-tail” feature. Only a small fraction, say 5%, of a site’s products are ever browsed or bought by customers, leaving no data on the remaining products. Additionally, customer sessions tend to be brief, limiting the amount of information we can get from any one individual. This issue is particularly acute for “data-hungry” models, which may not have sufficient training data with enough variation to accurately match products with customers.

My proposed solution to this issue is to recommend products that also encourage further exploration. Economic studies have shown that certain types of information structure can motivate customers to consider more options, harnessing the “wisdom of crowds” . Imagine two products: recommending the first leads to a 5% purchase likelihood, while the second has a 4% chance. But the second item prompts the customer to look at 5 additional products. This extra data allows our model to learn more, potentially enhancing recommendations for this and other customers in the future. Therefore, we might choose to recommend the second product to generate more user-driven training data.

In this project, we consider the multi-task learning that achieves better performance along the entire customer journey. The conventional conversion rate based model estimates

\[P(conversion|click, impression, u_i, v_j)\]

where \(u_i\) are users’ features and \(v_j\) are items’ features.

We decompose the conversion rate into

\[P(conversion, click|impression, u_i, v_j) = P(click|impression, u_i, v_j) \times P(convsersion|click, u_i, v_j)\]

Hence, we have two auxiliary tasks for predicting both the click-through rate and the conversion rate. Such approach has two advantages. First, the task for estimating the click-through rate generally has richer training data because we train on dataset with all impressions instead of the subsample with purchase. Second, we recommend products with both high probability of clicking and purchasing, leading to more training data points in future time periods. This can help us tackle the challenge of data sparsity .

Literature

Recommender Systems are usually classified into three categories : (i) collaborative filtering (ii) content-based ,and (iii) hybrid.

  1. Collaborative filtering. The input for the algorithm can be [User, Item, Outcome, Timestamp]. The task is to complete the matrix \(R\), where each column is an item and each row is a user, with the majority of missing elements. The memory based collaborative filtering finds pairs of user \(i\) and \(i'\) using similarity metrics The model based collaborative filtering decomposes \(R^{m\times n} = U^{m\times k}I^{k\times n}\) using matrix factorization, where \(k\) is the dimension of latent factors.

  2. Content-based. The input for the algorithm can be [User features, Item features, Outcome]. The task is to predict \(y=f(u_i, v_j)\), where \(y\) is the outcome and \(u_i\) and \(v_j\) are features of users and items respectively.

  3. Hybrid. we consider a simple linear model :

\[r_{ij} = x_{ij}\mu+z_i\gamma_j+w_j\lambda_i+\epsilon_{ij}\]

where \(x_{ij}\) is the collaborative filtering component indicating the interaction, \(z_i\) are users’ features and \(w_j\) are items’ feature. \(\gamma_j\) and \(\lambda_i\) are random coefficients. We can also apply matrix factorization to reduce the dimension of interaction matrix \(x_{ij}\). A recent application in marketing can be found in .

The core idea in collaborative filtering is “Similar consumers like similar products”. The similarity is defined on consumers’ revealed preference. However, the content-based approach implicitly assumes users and items should be similar if they are neighborhoods in feature space, which may or may not be true. The limitation of collaborative filtering is that we require a sufficient amount of interaction data, which is hard if we consider the sparsity and cold start problems.

Moreover, deep learning based recommender systems have gained significant attention by capturing the non-linear and non-trivial user-item relationships, and enable the codification of more complex abstractions as data representations in the higher layers. A nice survey for deep learning based recommender system can be found in . Deep learning based recommender system can have several strength compared to conventional models:

  1. It’s possible to capture complex non-linear user-item interactions. For example, when we model collaborative filtering by matrix factorization, we essentially use the low-dimensional linear model. The non-linear property makes it possible to deal with complex interaction patterns and precisely reflect user’s preference .

  2. Architecture, such as RNN and CNN, are widely applicable and flexible in mining sequential structure in data. For example, presented a co-evolutionary latent model to capture the co-evolution nature of users’ and items’ latent features. There are works dealing with the temporal dynamics of interactions and sequential patterns of user behaviours using CNN or RNN .

  3. Representation learning can be an effective method to learn the latent factor models that are widely used in recommender systems. There are works that incorporate methods such as autoencoder in traditional recommender system frameworks we summarize above. For example, autoencoder based collaborative filtering , and adversarial network (GAN) based recommendation .

Model

We implement the multi-task learning similar to :

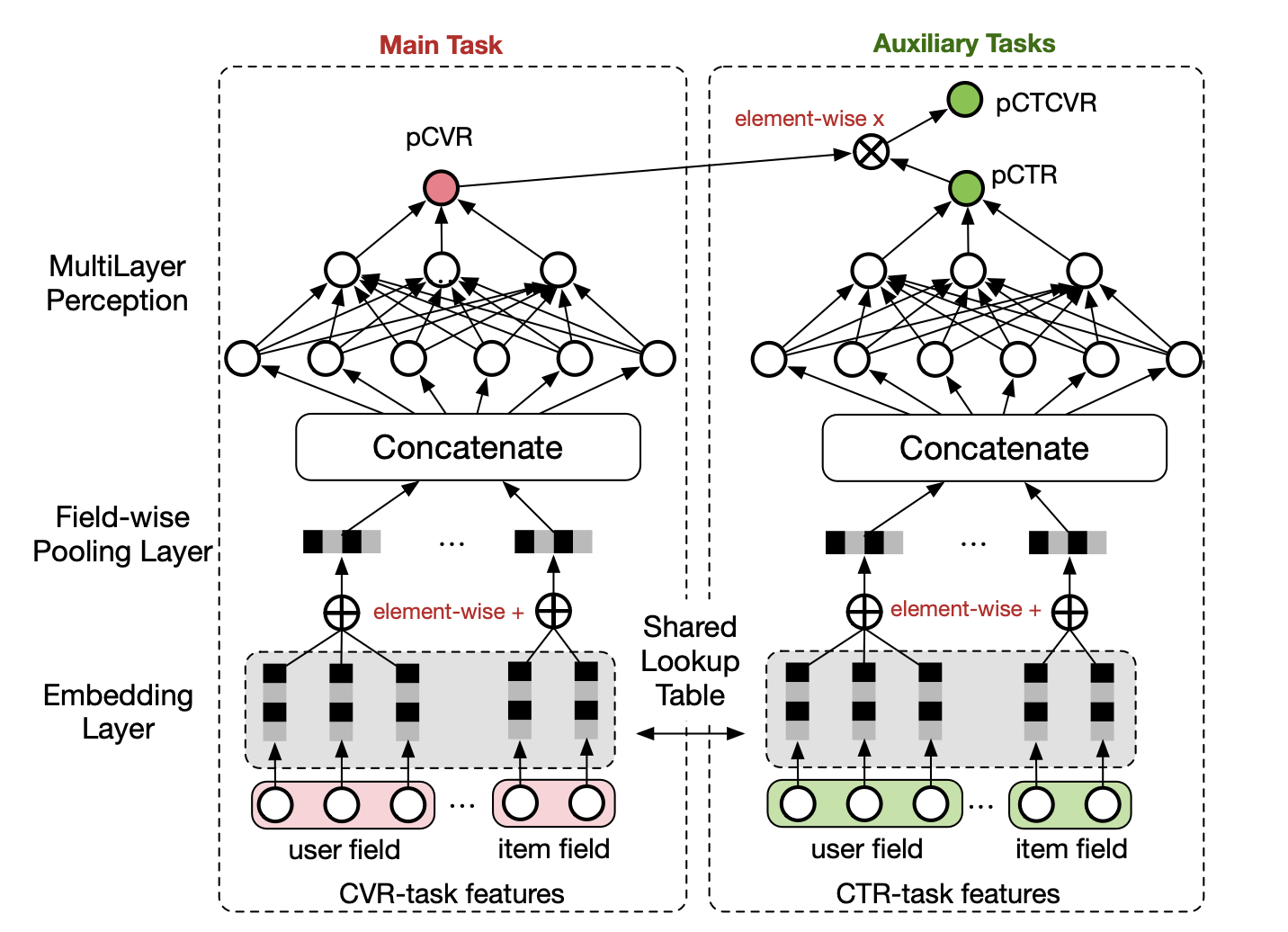
However, we differ from the model in in two ways:

  1. For user field, we implement RNN to deal with the sequential clickstream data instead of simple MLP.

  2. We define the loss function over the over samples of all impressions. The loss of conversion rate task and the loss of click-through rate task will not be used separately because both of them are based on subsamples (conditional on click and conditional on purchase).

\[L(\theta_{click}, \theta_{convsersion})=\sum_{i=1}^N l(click_i, f(u_i, v_j))+\sum_{i=1}^N l(click_i, purchase_i, f(u_i, v_j))\]

Experiment

The dataset we use is a random subsample from , which is the traffic logs from Taobao’s recommender system. We do a 1% random sampling, though the public dataset in has already been a 1% random sampling of the raw data. The summary statistics of the data can be found in .

For the performance metrics, we use Area under the ROC curve (AUC).

Several benchmark models we use for comparsion:

  1. DeepFM . This is a factorization-machine based neural network for click-through rate prediction. In my setting, I consider it as a single-task model with MLP structure.

  2. MMOE . This is the multi-task setting. However, since the usecase is MovieLens, where two tasks are “finish” and “like”, it doesn’t consider the type of sequential data. In my setting, I consider it as a multi-task model with MLP structure.

  3. xDeepFM . This model Combines both explicit and implicit feature interactions for recommender systems using a novel Compressed Interaction Network(CIN), which shares some functionalities with CNNs and RNNs. In my setting, I consider it as a single-task model with RNN/CNN structure.

  4. Our Model, a multi-task model with RNN/CNN structure.

Results:

Model test AUC test click AUC test conversion AUC
DeepFM 0.3233    
MMOE   0.5303 0.6053
xDeepFM 0.4093    
Ours   0.5505 0.6842